The Debye–Hückel limiting law
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص 163-165
2025-11-15
29
The Debye–Hückel limiting law
The long range and strength of the Coulombic interaction between ions means that it is likely to be primarily responsible for the departures from ideality in ionic solutions and to dominate all the other contributions to nonideality. This domination is the basis of the Debye–Hückel theory of ionic solutions, which was devised by Peter Debye and Erich Hückel in 1923. We give here a qualitative account of the theory and its principal conclusions. The calculation itself, which is a profound example of how a seemingly intractable problem can be formulated and then resolved by drawing on physical insight, is described in Further information 5.1. Oppositely charged ions attract one another. As a result, anions are more likely to be found near cations in solution, and vice versa (Fig. 5.33). Overall, the solution is electrically neutral, but near any given ion there is an excess of counter ions (ions of opposite charge). Averaged over time, counter ions are more likely to be found near any given ion. This time-averaged, spherical haze around the central ion, in which counter ions outnumber ions of the same charge as the central ion, has a net charge equal in magnitude but opposite in sign to that on the central ion, and is called its ionic atmosphere. The energy, and therefore the chemical potential, of any given central ion is lowered as a result of its electrostatic interaction with its ionic atmosphere. This lowering of energy appears as the difference between the molar Gibbs energy Gm and the ideal value Gm ideal of the solute, and hence can be identified with RT ln γ±. The stabilization of ions by their interaction with their ionic atmospheres is part of the explanation why chemists commonly use dilute solutions, in which the stabilization is less important, to achieve precipitation of ions from electrolyte solutions. The model leads to the result that at very low concentrations the activity coefficient can be calculated from the Debye–Hückel limiting law
log γ± =−|z+z−|AI1/2
where A = 0.509 for an aqueous solution at 25°C and I is the dimensionless ionic strength of the solution:
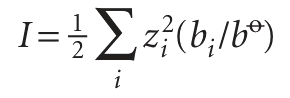
In this expression zi is the charge number of an ion i (positive for cations and negative for anions) and bi is its molality. The ionic strength occurs widely wherever ionic solutions are discussed, as we shall see. The sum extends over all the ions present in the solution. For solutions consisting of two types of ion at molalities b+ and b−,
I = 1–2(b+z+2 + b−z−2)/bo
The ionic strength emphasizes the charges of the ions because the charge numbers occur as their squares. Table 5.4 summarizes the relation of ionic strength and molality in an easily usable form.
The name ‘limiting law’ is applied to eqn 5.69 because ionic solutions of moderate molalities may have activity coefficients that differ from the values given by this expression, yet all solutions are expected to conform as b → 0. Table 5.5 lists some experimental values of activity coefficients for salts of various valence types.
Figure 5.34 shows some of these values plotted against I1/2, and compares them with the theoretical straight lines calculated from eqn 5.69. The agreement at very low molalities (less than about 1 mmol kg−1, depending on charge type) is impressive, and convincing evidence in support of the model. Nevertheless, the departures from the theoretical curves above these molalities are large, and show that the approximations are valid only at very low concentrations.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
