Ideal solutions
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص143-144
2025-11-13
65
Ideal solutions
We shall denote quantities relating to pure substances by a superscript *, so the chemical potential of pure A is written µA*, and as µA*(l) when we need to emphasize that A is a liquid. Because the vapour pressure of the pure liquid is pA*, it follows from eqn 5.14 that the chemical potential of A in the vapour (treated as a perfect gas) is µA 7 +RT ln pA* (with pA to be interpreted as the relative pressure pA/p7). These two chemical potentials are equal at equilibrium (Fig. 5.10), so we can write
µA* = µAO+ RT ln pA
If another substance, a solute, is also present in the liquid, the chemical potential of A in the liquid is changed to µA and its vapour pressure is changed to pA. The vapour and solvent are still in equilibrium, so we can write
µA =µAO +RT ln pA
Next, we combine these two equations to eliminate the standard chemical potential of the gas. To do so, we write eqn 5.21 as µAO = µA* – RT ln pA* and substitute this expression into eqn 5.22 to obtain
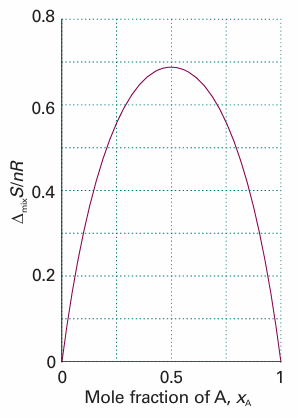
Fig. 5.9 The entropy of mixing of two perfect gases and (as discussed later) of two liquids that form an ideal solution. The entropy increases for all compositions and temperatures, so perfect gases mix spontaneously in all proportions. Because there is no transfer of heat to the surroundings when perfect gases mix, the entropy of the surroundings is unchanged. Hence, the graph also shows the total entropy of the system plus the surroundings when perfect gases mix.
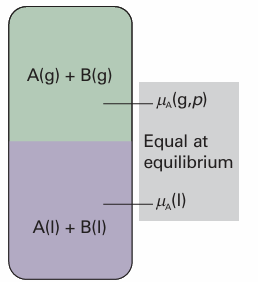
Fig. 5.10 At equilibrium, the chemical potential of the gaseous form of a substance A is equal to the chemical potential of its condensed phase. The equality is preserved if a solute is also present. Because the chemical potential of A in the vapour depends on its partial vapour pressure, it follows that the chemical potential of liquid A can be related to its partial vapour pressure.
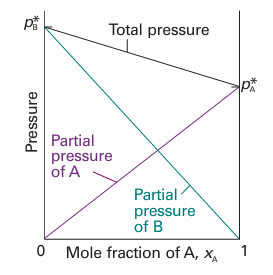
Fig. 5.11 The total vapour pressure and the two partial vapour pressures of an ideal binary mixture are proportional to the mole fractions of the components.
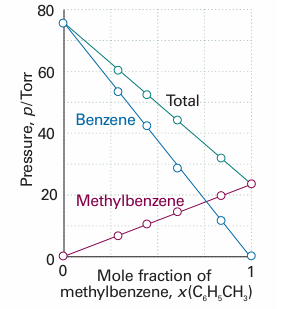
Fig. 5.12 Two similar liquids, in this case benzene and methylbenzene (toluene), behave almost ideally, and the variation of their vapour pressures with composition resembles that for an ideal solution.
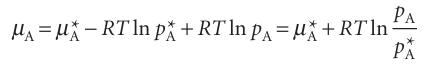
In the final step we draw on additional experimental information about the relation between the ratio of vapour pressures and the composition of the liquid. In a series of experiments on mixtures of closely related liquids (such as benzene and methylbenzene), the French chemist François Raoult found that the ratio of the partial vapour pressure of each component to its vapour pressure as a pure liquid, pA/pA*, is approximately equal to the mole fraction of A in the liquid mixture. That is, he established what we now call Raoult’s law:
pA =xApA*
This law is illustrated in Fig. 5.11. Some mixtures obey Raoult’s law very well, especially when the components are structurally similar (Fig. 5.12). Mixtures that obey the law throughout the composition range from pure A to pure B are called ideal solutions. When we write equations that are valid only for ideal solutions, we shall label them with a superscript °, as in eqn 5.24. For an ideal solution, it follows from eqns 5.23 and 5.24 that
µA = µA* +RT ln xA
This important equation can be used as the definition of an ideal solution (so that it implies Raoult’s law rather than stemming from it). It is in fact a better definition than eqn 5.24 because it does not assume that the vapour is a perfect gas.
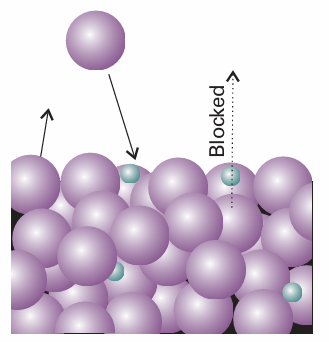
Fig. 5.13 A pictorial representation of the molecular basis of Raoult’s law. The large spheres represent solvent molecules at the surface of a solution (the uppermost line of spheres), and the small spheres are solute molecules. The latter hinder the escape of solvent molecules into the vapour, but do not hinder their return.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
