Other thermodynamic mixing functions
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
143
2025-11-13
72
Other thermodynamic mixing functions
Because (∂G/∂T) p,n =−S, it follows immediately from eqn 5.18 that, for a mixture of perfect gases initially at the same pressure, the entropy of mixing, ∆mixS, is
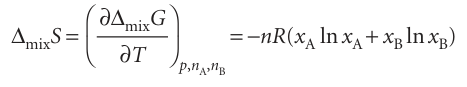
Because ln x < 0, it follows that ∆mixS > 0 for all compositions (Fig. 5.9). For equal amounts of gas, for instance, we set xA = xB = 1–2, and obtain ∆mixS = nR ln 2, with n the total amount of gas molecules. This increase in entropy is what we expect when one gas disperses into the other and the disorder increases. We can calculate the isothermal, isobaric (constant pressure) enthalpy of mixing, ∆mixH, the enthalpy change accompanying mixing, of two perfect gases from ∆G = ∆H−T∆S. It follows from eqns 5.18 and 5.19 that
∆mixH =0
The enthalpy of mixing is zero, as we should expect for a system in which there are no interactions between the molecules forming the gaseous mixture. It follows that the whole of the driving force for mixing comes from the increase in entropy of the system, because the entropy of the surroundings is unchanged.
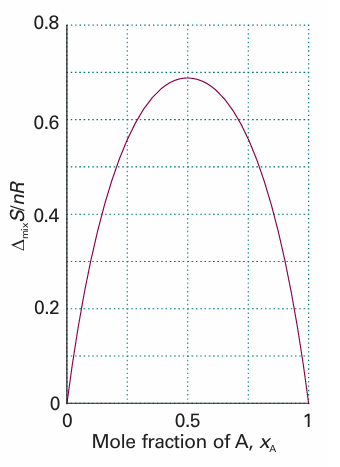
Fig. 5.9 The entropy of mixing of two perfect gases and (as discussed later) of two liquids that form an ideal solution. The entropy increases for all compositions and temperatures, so perfect gases mix spontaneously in all proportions. Because there is no transfer of heat to the surroundings when perfect gases mix, the entropy of the surroundings is unchanged. Hence, the graph also shows the total entropy of the system plus the surroundings when perfect gases mix.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
