The Gibbs energy of mixing of perfect gases
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص141-142
2025-11-13
69
The Gibbs energy of mixing of perfect gases
Let the amounts of two perfect gases in the two containers be nA and nB; both are at a temperature T and a pressure p (Fig. 5.6). At this stage, the chemical potentials of the two gases have their ‘pure’ values, which are obtained by applying the definition µ=Gm to eqn 3.57:
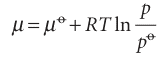
where µo is the standard chemical potential, the chemical potential of the pure gas at 1 bar. It will be much simpler notationally if we agree to let p denote the pressure relative to po; that is, to replace p/po by p, for then we can write
µ=µo+ RT ln p
Equations for which this convention is used will be labelled {1}, {2},...; to use the equations, we have to remember to replace p by p/po again. In practice, that simply means using the numerical value of p in bars. The Gibbs energy of the total system is then given by eqn 5.5 as
Gi =nAµA+nBµB=nA (µAo +RT ln p) +nB (µBo +RT ln p)
After mixing, the partial pressures of the gases are pA and pB, with pA + pB=p. The total Gibbs energy changes to
Gf=nA (µAo+ RT ln pA)+nB(µB o+ RT ln pB)
The difference Gf−Gi, the Gibbs energy of mixing, ∆mix G, is therefore
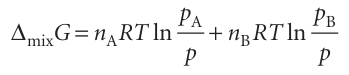
At this point we may replace nJ by xJn, where nis the total amount of A and B, and use the relation between partial pressure and mole fraction (Section 1.2b) to write pJ/p=xJ for each component, which gives
∆mixG=nRT (xAlnxA + xBlnxB)
Because mole fractions are never greater than 1, the logarithms in this equation are negative, and ∆mixG
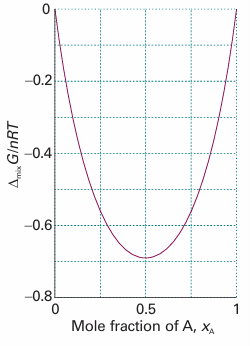
Fig. 5.7The Gibbs energy of mixing of two perfect gases and (as discussed later) of two liquids that form an ideal solution. The Gibbs energy of mixing is negative for all compositions and temperatures, so perfect gases mix spontaneously in all proportions.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
