Excess functions and regular solutions
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص149-150
2025-11-13
69
Excess functions and regular solutions
The thermodynamic properties of real solutions are expressed in terms of the excess functions, XE, the difference between the observed thermodynamic function of mixing and the function for an ideal solution. The excess entropy, SE, for example, is defined as
SE =∆mixS −∆mixSideal
where ∆mixSideal is given by eqn 5.28. The excess enthalpy and volume are both equal to the observed enthalpy and volume of mixing, because the ideal values are zero in each case. Deviations of the excess energies from zero indicate the extent to which the solutions are nonideal. In this connection a useful model system is the regular solution, a solution for which HE≠0 but SE=0. We can think of a regular solution as one in which the two kinds of molecules are distributed randomly (as in an ideal solution) but have different energies of interactions with each other. Figure 5.18 shows two examples of the composition dependence of molar excess functions. We can make this discussion more quantitative by supposing that the excess en thalpy depends on composition as
HE=nβRTxAxB
where β is a dimensionless parameter that is a measure of the energy of AB inter actions relative to that of the AA and BB interactions. The function given by eqn 5.30 is plotted in Fig. 5.19, and we see it resembles the experimental curve in Fig. 5.18. If β<0 mixing is exothermic and the solute–solvent interactions are more favourable than the solvent–solvent and solute–solute interactions. If β > 0, then the mixing is
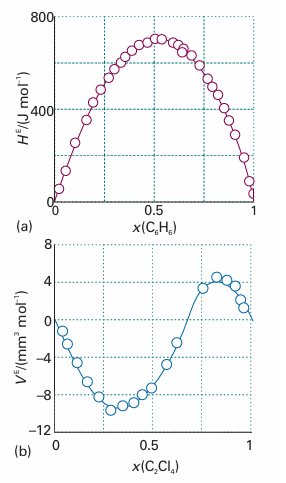
Fig. 5.18 Experimental excess functions at 25°C. (a) HE for benzene/cyclohexane; this graph shows that the mixing is endothermic (because ∆mixH = 0 for an ideal solution). (b) The excess volume, VE, for tetrachloroethene/cyclopentane; this graph shows that there is a contraction at low tetrachloroethane mole fractions, but an expansion at high mole fractions (because ∆mixV = 0 for an ideal mixture).
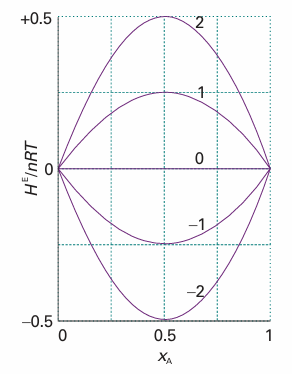
Fig. 5.19 The excess enthalpy according to a model in which it is proportional to βxAxB, for different values of the parameter β.
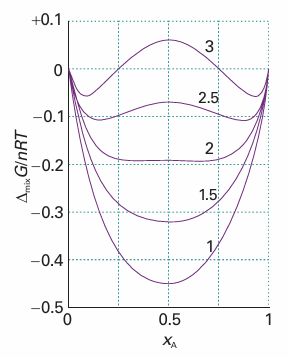
Fig. 5.20 The Gibbs energy of mixing for different values of the parameter β.
endothermic. Because the entropy of mixing has its ideal value for a regular solution, the excess Gibbs energy is equal to the excess enthalpy, and the Gibbs energy of mixing is
∆mixG =nRT {xAlnxA + xBlnxB + βxAxB}
Figure 5.20 shows how ∆mixG varies with composition for different values of β. The important feature is that for β > 2 the graph shows two minima separated by a maximum. The implication of this observation is that, provided β > 2, then the system will separate spontaneously into two phases with compositions corresponding to the two minima, for that separation corresponds to a reduction in Gibbs energy. We develop this point in Sections 5.8 and 6.5.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
