


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-12-2021
Date: 15-10-2021
Date: 30-8-2021
|

Consider three mutually tangent circles, and draw their inner Soddy circle. Then draw the inner Soddy circles of this circle with each pair of the original three, and continue iteratively. The steps in the process are illustrated above (Trott 2004, pp. 34-35).
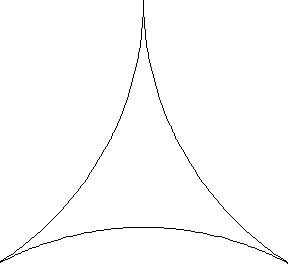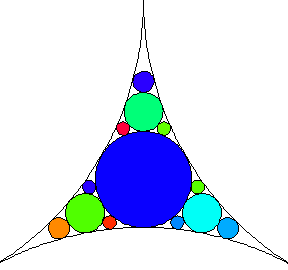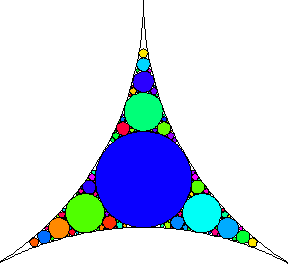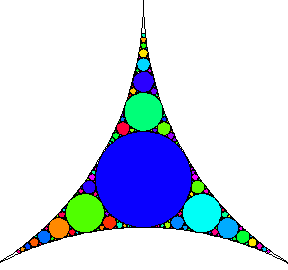
An animation illustrating the construction of the gasket is shown above.
The points which are never inside a circle form a set of measure 0 having fractal dimension approximately 1.3058 (Mandelbrot 1983, p. 172). The Apollonian gasket corresponds to a limit set that is invariant under a Kleinian group (Wolfram 2002, p. 986).

The Apollonian gasket can also be generalized to three dimensions (Boyd 1973, Andrade et al. 2005), as illustrated above. A graph obtained by connecting the centers of touching spheres in a three-dimensional Apollonian gasket by edges is known as an Apollonian network.
REFERENCES:
Andrade, J. S. Jr.; Herrmann, H. J.; Andrade, R. F. S.; 2 and da Silva, L. R. "Apollonian Networks: Simultaneously Scale-Free, Small World, Euclidean, Space Filling, and with Matching Graphs." Phys. Rev. Lett. 94, 01870-1-4, 2005.
Boyd, D. W. "Improved Bounds for the Disk Packing Constants." Aeq. Math. 9, 99-106, 1973.
Boyd, D. W. "The Residual Set Dimension of the Apollonian Packing." Mathematika 20, 170-174, 1973.
Boyd, D. W. "The Osculatory Packing of a Three Dimensional Sphere." Canad. J. Math. 25, 303-322, 1973.
Kasner, E. and Supnick, F. "The Apollonian Packing of Circles." Proc. Nat. Acad. Sci. USA 29, 378-384, 1943.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 169-172, 1983.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 3-4, 1991.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 986, 2002.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|