Regge Calculus

Regge calculus is a finite element method utilized in numerical relativity in attempts of describing spacetimes with few or no symmetries by way of producing numerical solutions to the Einstein field equations (Khavari 2009). It was developed initially by Italian mathematician Tullio Regge in the 1960s (Regge 1961).

Modern forays into Regge's method center on the triangulation of manifolds, particularly on the discrete approximation of 4-dimensional Riemannian and Lorentzian manifolds by way of cellular complexes whose 4-dimensional triangular simplices share their boundary tetrahedra (i.e., 3-dimensional simplices) to enclose a flat piece of spacetime (Marinelli 2013). Worth noting is that Regge himself devised the framework in more generality, though noted that no such generality is lost by assuming a triangular approximation (Regge 1961).

The benefit of this technique is that the structures involved are rigid and hence are completely determined once their edge lengths have been specified (Khavari 2009). On the other hand, this method is inherently more difficult due to the fact that many of the fundamental properties on a given spacetime (e.g., its topology, its metric tensor, its curvature, etc.) are dependent upon the smoothness of the underlying manifold structure.

Intuitively, the gap between a crude spacetime approximation and the smoothness of the underlying manifold can be bridged by viewing the manifold as the limit of a sequence of these piecewise-linear approximations; this is done by increasing the number of lower-dimensional simplices used to approximate and by passing to a limit. With this in mind, the study of relativity by way of Regge calculus requires a discretization of all spacetime-related structures (i.e., topology, metric tensor, curvature, etc.) to which some suitable limiting process can be applied in order to obtain the smooth versions thereof. A key aspect is to notice that the curvature of a smooth manifold is intuitively reflected in the codimension-2 sub-simplices--called hinges or bones within Regge's framework--of any simplicial approximation thereof. Hinges in a 4-dimensional simplex 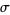 are 2-dimensional simplices, e.g., triangles, and the amount of curvature residing on a hinge  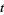is represented by its so-called deficit angle (or deficiency)  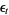(Khavari 2009). A positive, respectively negative, value of  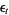represents positive, respectively negative, manifold curvature. From here, Regge's theory develops by discretizing the relativistic gravitational action, Einstein's vacuum field equations, the Bianchi identities, etc., and by adapting the discretization techniques for Riemannian manifolds (as outlined above) to Lorentzian manifolds, e.g., to Minkowski Space.

Since Regge's original work, a number of improvements and extensions have been discovered, including explicit algorithms for computing dihedral and deficit angles for arbitrary discretized manifolds and generalizations intended to factor in more advanced physical phenomena.

Though generally accepted as a worthwhile technique, Regge's method isn't without its detractors. Indeed, recent literature has shown some unexpected behavior of Regge's discretized theory of relativity in limiting cases (Brewin and Gentle). What's more, various difficulties inherent to the theory itself have relegated Regge calculus to the role of regenerating known solutions to Einstein's field equations without it ever having been applied the evolutionary behavior, etc., of arbitrary manifolds (Khavari 2009). Despite the fact that Regge calculus has been identified as an important tool to understand both classical gravity and the modern models of quantum gravity (Marinelli 2013), its usefulness has remained unexplored (Khavari 2009). Regardless, the technique has become increasingly important in the study of modern physics, even proving fruitful in areas of mathematics not typically associated to relativity (Williams 1991).

REFERENCES:

Bahr, B. and Dittich, B. "Regge Calculus from a New Angle." 2009. https://arxiv.org/abs/0907.4325.

Brewin, L. C. and Gentle, A. P. "On the Convergence of Regge Calculus to General Relativity." Class. Q. Grav. 18, 517-525, 2001.

Khavari, P. "Regge Calculus as a Numerical Approach to General Relativity." 2009. https://www.astro.utoronto.ca/theses/thesis09.khavari.pdf.

Marinelli, D. "A Practical Look at Regge Calculus." 2013. https://fias.uni-frankfurt.de/~nicolini/slides/Marinelli.pdf.

Regge, T. "General Relativity Without Coordinates." Il Nuovo Cimento XIX, 558-571, 1961.

Williams, R. M. "Discrete Quantum Gravity: The Regge Calculus Approach." 1991. https://cds.cern.ch/record/230326/files/th-6236-91.pdf.