المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Thâbit ibn Kurrah Prime |
 573
 03:33 مساءً
date: 30-9-2020 |
Author : Sloane, N. J. A. 
Book or Source : Sequences A002235/M0545 and A055010 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 17-8-2020
602
Date: 29-11-2020
978
Date: 23-11-2019
1925
|
A Thâbit ibn Kurrah prime, sometimes called a 321-prime, is a Thâbit ibn Kurrah number (i.e., a number of the form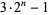 
for nonnegative integer 
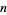) that is prime.
The indices for the first few Thâbit ibn Kurrah primes are 0, 1, 2, 3, 4, 6, 7, 11, 18, 34, 38, 43, 55, 64, 76, 94, 103, 143, 206, 216, 306, 324, 391, 458, 470, ... (OEIS A002235), corresponding to the primes 2, 5, 11, 23, 47, 191, 383, 6143, ... (OEIS A007505).
Riesel (1969) extended the search to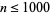 
. A search for larger primes was coordinated by P. Underwood. PrimeGrid has continued that search and has checked values of 
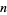up to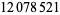 
as of Nov. 2015 (PrimeGrid). The table below summarizes the largest known Thâbit ibn Kurrah primes.
 |
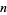digits | discoverer |
 |
 |
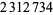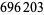PrimeGrid (Dec. 2005; https://primes.utm.edu/primes/page.php?id=76506) |
 |
 |
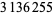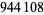PrimeGrid (Mar. 2007; https://primes.utm.edu/primes/page.php?id=79671) |
 |
 |
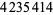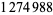PrimeGrid (Apr. 2008; https://primes.utm.edu/primes/page.php?id=84769) |
 |
 |
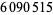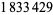PrimeGrid (Apr. 2010; https://primes.utm.edu/primes/page.php?id=92517) |
 |
 |
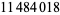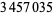PrimeGrid (Nov. 2014; https://primes.utm.edu/primes/page.php?id=118807) |
 |
 |
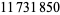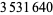PrimeGrid (Mar. 2015; https://primes.utm.edu/primes/page.php?id=119571) |
 |
 |
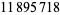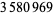PrimeGrid (Jun. 6, 2015; https://primes.utm.edu/primes/page.php?id=120038) |
REFERENCES:
Caldwell, C. https://primes.utm.edu/primes/search.php?Description=%5E3*2%5E%-1&Style=HTML.
PrimeGrid. "BOINC Status: Subproject Status: LLR: 321 Prime Search." https://www.primegrid.com/server_status_subprojects.php.
PrimeGrid. "PrimeGrid Primes: Subproject: (321) 321 Prime Search." https://www.primegrid.com/primes/primes.php?project=321.
Riesel, H. "Lucasian Criteria for the Primality of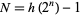 
." Math. Comput. 23, 869-875, 1969.
Sloane, N. J. A. Sequences A002235/M0545 and A055010 in "The On-Line Encyclopedia of Integer Sequences."
Underwood, P. "321 Statistics." 14 Dec 2004. https://www.mersenneforum.org/showthread.php?t=3410.
Underwood, P. "321 Search." https://www.mersenneforum.org/321search/.
Underwood, P. https://www.mersenneforum.org/321search/The%20status%20of%20the%20search.html.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
