


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2020
Date: 24-9-2020
Date: 11-10-2020
|
The decimal expansion of a number is its representation in base-10 (i.e., in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the 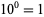 s place. For example, the number with decimal expansion 1234.56 is defined as
s place. For example, the number with decimal expansion 1234.56 is defined as
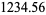 |
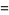 |
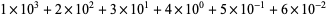 |
(1) |
 |
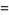 |
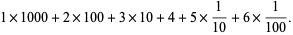 |
(2) |
Expressions written in this form 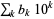 (where negative
(where negative 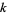 are allowed as exemplified above but usually not considered in elementary education contexts) are said to be in expanded notation.
are allowed as exemplified above but usually not considered in elementary education contexts) are said to be in expanded notation.
Other examples include the decimal expansion of 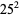 given by 625, of
given by 625, of 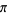 given by 3.14159..., and of
given by 3.14159..., and of 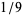 given by 0.1111.... The decimal expansion of a number can be found in the Wolfram Language using the command RealDigits[n], or equivalently, RealDigits[n, 10].
given by 0.1111.... The decimal expansion of a number can be found in the Wolfram Language using the command RealDigits[n], or equivalently, RealDigits[n, 10].
The decimal expansion of a number may terminate (in which case the number is called a regular number or finite decimal, e.g., 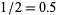 ), eventually become periodic (in which case the number is called a repeating decimal, e.g.,
), eventually become periodic (in which case the number is called a repeating decimal, e.g., 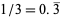 ), or continue infinitely without repeating (in which case the number is called irrational).
), or continue infinitely without repeating (in which case the number is called irrational).
The following table summarizes the decimal expansions of the first few unit fractions. As usual, the repeating portion of a decimal expansion is conventionally denoted with a vinculum.
| fraction | decimal expansion | fraction | decimal expansion |
| 1 | 1 | 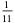 |
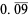 |
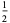 |
0.5 | 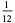 |
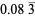 |
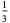 |
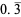 |
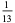 |
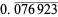 |
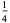 |
0.25 | 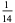 |
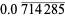 |
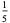 |
0.2 | 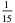 |
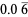 |
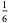 |
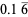 |
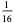 |
0.0625 |
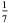 |
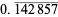 |
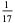 |
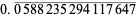 |
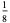 |
0.125 | 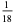 |
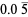 |
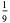 |
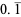 |
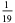 |
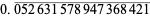 |
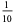 |
0.1 | 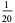 |
0.05 |
If 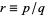 has a finite decimal expansion (i.e.,
has a finite decimal expansion (i.e., 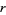 is a regular number), then
is a regular number), then
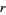 |
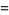 |
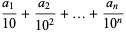 |
(3) |
 |
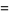 |
 |
(4) |
 |
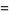 |
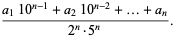 |
(5) |
Factoring possible common multiples gives
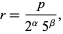 |
(6) |
where 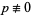 (mod 2, 5). Therefore, the numbers with finite decimal expansions are fractions of this form. The first few regular numbers are 1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, ... (OEIS A003592).
(mod 2, 5). Therefore, the numbers with finite decimal expansions are fractions of this form. The first few regular numbers are 1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, ... (OEIS A003592).
Any nonregular fraction 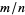 is periodic, and has a decimal period
is periodic, and has a decimal period 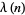 independent of
independent of 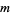 , which is at most
, which is at most 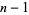 digits long. If
digits long. If 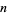 is relatively prime to 10, then the period
is relatively prime to 10, then the period 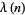 of
of 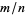 is a divisor of
is a divisor of 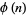 and has at most
and has at most 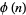 digits, where
digits, where 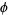 is the totient function. It turns out that
is the totient function. It turns out that 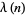 is the multiplicative order of 10 (mod
is the multiplicative order of 10 (mod 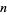 ) (Glaisher 1878, Lehmer 1941). The number of digits in the repeating portion of the decimal expansion of a rational number can also be found directly from the multiplicative order of its denominator.
) (Glaisher 1878, Lehmer 1941). The number of digits in the repeating portion of the decimal expansion of a rational number can also be found directly from the multiplicative order of its denominator.
When a rational number 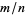 with
with 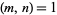 is expanded, the period begins after
is expanded, the period begins after 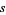 terms and has length
terms and has length 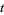 , where
, where 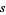 and
and 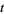 are the smallest numbers satisfying
are the smallest numbers satisfying
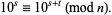 |
(7) |
When 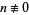 (mod 2, 5),
(mod 2, 5), 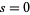 , and this becomes a purely periodic decimal with
, and this becomes a purely periodic decimal with
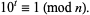 |
(8) |
As an example, consider 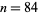 .
.
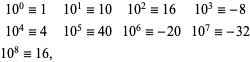 |
(9) |
so 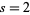 ,
, 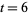 . The decimal representation is
. The decimal representation is 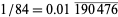 . When the denominator of a fraction
. When the denominator of a fraction 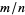 has the form
has the form 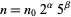 with
with 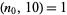 , then the period begins after
, then the period begins after 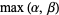 terms and the length of the period is the exponent to which 10 belongs (mod
terms and the length of the period is the exponent to which 10 belongs (mod 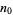 ), i.e., the number
), i.e., the number  such that
such that 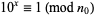 . If
. If 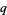 is prime and
is prime and 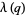 is even, then breaking the repeating digits into two equal halves and adding gives all 9s. For example,
is even, then breaking the repeating digits into two equal halves and adding gives all 9s. For example, 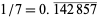 , and
, and 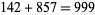 . For
. For 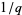 with a prime denominator other than 2 or 5, all cycles
with a prime denominator other than 2 or 5, all cycles 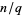 have the same length (Conway and Guy 1996).
have the same length (Conway and Guy 1996).
If 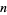 is a prime and 10 is a primitive root of
is a prime and 10 is a primitive root of 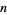 , then the period
, then the period 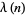 of the repeating decimal
of the repeating decimal 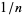 is given by
is given by
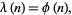 |
(10) |
where 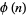 is the totient function. Furthermore, the decimal expansions for
is the totient function. Furthermore, the decimal expansions for 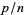 , with
, with 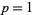 , 2, ...,
, 2, ..., 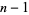 have periods of length
have periods of length 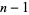 and differ only by a cyclic permutation. Such numbers
and differ only by a cyclic permutation. Such numbers 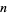 are called full reptend primes.
are called full reptend primes.
To find denominators with short periods, note that
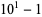 |
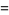 |
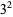 |
(11) |
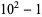 |
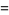 |
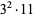 |
(12) |
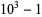 |
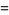 |
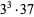 |
(13) |
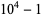 |
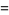 |
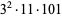 |
(14) |
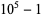 |
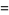 |
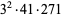 |
(15) |
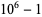 |
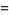 |
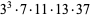 |
(16) |
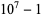 |
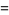 |
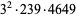 |
(17) |
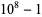 |
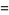 |
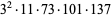 |
(18) |
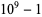 |
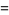 |
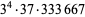 |
(19) |
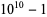 |
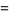 |
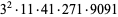 |
(20) |
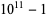 |
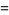 |
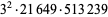 |
(21) |
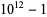 |
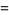 |
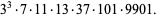 |
(22) |
The decimal period of a fraction with denominator equal to a prime factor above is therefore the power of 10 in which the factor first appears. For example, 37 appears in the factorization of 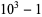 and
and 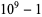 , so its period is 3. Multiplication of any factor by a
, so its period is 3. Multiplication of any factor by a 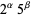 still gives the same period as the factor alone. A denominator obtained by a multiplication of two factors has a period equal to the first power of 10 in which both factors appear. The following table gives the primes having small periods (OEIS A007138, A046107, and A046108; Ogilvy and Anderson 1988).
still gives the same period as the factor alone. A denominator obtained by a multiplication of two factors has a period equal to the first power of 10 in which both factors appear. The following table gives the primes having small periods (OEIS A007138, A046107, and A046108; Ogilvy and Anderson 1988).
| period | primes |
| 1 | 3 |
| 2 | 11 |
| 3 | 37 |
| 4 | 101 |
| 5 | 41, 271 |
| 6 | 7, 13 |
| 7 | 239, 4649 |
| 8 | 73, 137 |
| 9 | 333667 |
| 10 | 9091 |
| 11 | 21649, 513239 |
| 12 | 9901 |
| 13 | 53, 79, 265371653 |
| 14 | 909091 |
| 15 | 31, 2906161 |
| 16 | 17, 5882353 |
| 17 | 2071723, 5363222357 |
| 18 | 19, 52579 |
| 19 | 1111111111111111111 |
| 20 | 3541, 27961 |
A table of the periods 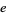 of small primes other than the special
of small primes other than the special 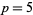 , for which the decimal expansion is not periodic, follows (OEIS A002371).
, for which the decimal expansion is not periodic, follows (OEIS A002371).
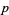 |
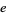 |
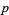 |
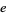 |
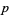 |
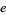 |
| 3 | 1 | 31 | 15 | 67 | 33 |
| 7 | 6 | 37 | 3 | 71 | 35 |
| 11 | 2 | 41 | 5 | 73 | 8 |
| 13 | 6 | 43 | 21 | 79 | 13 |
| 17 | 16 | 47 | 46 | 83 | 41 |
| 19 | 18 | 53 | 13 | 89 | 44 |
| 23 | 22 | 59 | 58 | 97 | 96 |
| 29 | 28 | 61 | 60 | 101 | 4 |
Shanks (1873ab) computed the periods for all primes up to 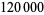 and published those up to
and published those up to 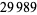 .
.
REFERENCES:
Conway, J. H. and Guy, R. K. "Fractions Cycle into Decimals." In The Book of Numbers. New York: Springer-Verlag, pp. 157-163 and 166-171, 1996.
Das, R. C. "On Bose Numbers." Amer. Math. Monthly 56, 87-89, 1949.
de Polignac, A. "Note sur la divisibilité des nombres." Nouv. Ann. Math. 14, 118-120, 1855.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 159-179, 2005.
Glaisher, J. W. L. "Periods of Reciprocals of Integers Prime to 10." Proc. Cambridge Philos. Soc. 3, 185-206, 1878.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 25, 2003.
Lehmer, D. H. "Guide to Tables in the Theory of Numbers." Bulletin No. 105. Washington, DC: National Research Council, pp. 7-12, 1941.
Lehmer, D. H. "A Note on Primitive Roots." Scripta Math. 26, 117-119, 1963.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, p. 60, 1988.
Rademacher, H. and Toeplitz, O. The Enjoyment of Mathematics: Selections from Mathematics for the Amateur. Princeton, NJ: Princeton University Press, pp. 147-163, 1957.
Rao, K. S. "A Note on the Recurring Period of the Reciprocal of an Odd Number." Amer. Math. Monthly 62, 484-487, 1955.
Shanks, W. "On the Number of Figures in the Period of the Reciprocal of Every Prime Number Below 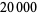 ." Proc. Roy. Soc. London 22, 200, 1873a.
." Proc. Roy. Soc. London 22, 200, 1873a.
Shanks, W. "On the Number of Figures in the Period of the Reciprocal of Every Prime Number Between 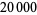 and
and 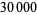 ." Proc. Roy. Soc. London 22, 384, 1873b.
." Proc. Roy. Soc. London 22, 384, 1873b.
Shiller, J. K. "A Theorem in the Decimal Representation of Rationals." Amer. Math. Monthly 66, 797-798, 1959.
Sloane, N. J. A. Sequences A002329/M4045, A002371/M4050, A003592, A007138/M2888, A046107, and A046108 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 60, 1986.



|
|
|
|
دور في الحماية من السرطان.. يجب تناول لبن الزبادي يوميا
|
|
|
|
|
|
|
العلماء الروس يطورون مسيرة لمراقبة حرائق الغابات
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|