Proper Divisor
المؤلف:
Derbyshire, J.
المصدر:
Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin
الجزء والصفحة:
...
29-11-2020
1590
Proper Divisor
A positive proper divisor is a positive divisor of a number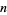 
, excluding 
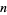itself. For example, 1, 2, and 3 are positive proper divisors of 6, but 6 itself is not. The number of proper divisors of 
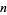is therefore given by
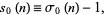where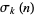 
is the divisor function. For 
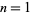, 2, ..., 
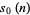is therefore given by 0, 1, 1, 2, 1, 3, 1, 3, 2, 3, ... (OEIS A032741). The largest proper divisors of 
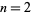, 3, ... are 1, 1, 2, 1, 3, 1, 4, 3, 5, 1, ... (OEIS A032742).
The term "proper divisor" is sometimes used to include negative integer divisors of a number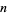 
(excluding 
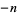). Using this definition, 
, 
, 
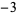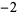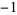, 1, 2, and 3 are the proper divisors of 6, while 
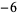and 6 are the improper divisors.
To make matters even more confusing, the proper divisor is often defined so that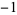 
and 1 are also excluded. Using this alternative definition, the proper divisors of 6 would then be 
, 
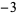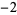, 2, and 3, and the improper divisors would be 
, 
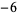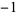, 1, and 6.
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 8-9, 2004.
Sloane, N. J. A. Sequences A032741 and A032742 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
