


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-11-2019
Date: 4-3-2020
Date: 1-11-2019
|
A generalization of Fermat's last theorem which states that if 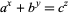 , where
, where 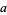 ,
, 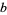 ,
, 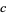 ,
,  ,
, 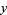 , and
, and 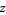 are any positive integers with
are any positive integers with 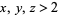 , then
, then 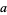 ,
, 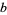 , and
, and 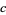 have a common factor. The conjecture was announced in Mauldin (1997), and a cash prize of
have a common factor. The conjecture was announced in Mauldin (1997), and a cash prize of 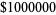 has been offered for its proof or a counterexample (Castelvecchi 2013).
has been offered for its proof or a counterexample (Castelvecchi 2013).
This conjecture is more properly known as the Tijdeman-Zagier conjecture (Elkies 2007).
REFERENCES:
Brun, V. "Über hypothesesenbildungen." Arc. Math. Naturvidenskab 34, 1-14, 1914.
Castelvecchi, D. "Mathematics Prize Ups the Ante to $1 Million." June 4, 2013. https://blogs.nature.com/news/2013/06/mathematics-prize-ups-the-ante-to-1-million.html.
Darmon, H. and Granville, A. "On the Equations 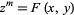 and
and 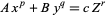 ." Bull. London Math. Soc. 27, 513-543, 1995.
." Bull. London Math. Soc. 27, 513-543, 1995.
Elkies, N. "The ABCs of Number Theory." Harvard Math. Rev. 1, 64-76, 2007.
Mauldin, R. D. "A Generalization of Fermat's Last Theorem: The Beal Conjecture and Prize Problem." Not. Amer. Math. Soc. 44, 1436-1437, 1997.
Mauldin, R. D. "The Beal Conjecture and Prize." https://www.math.unt.edu/~mauldin/beal.html.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|