The theory of relativity shows us that the relationships of positions and times as measured in one coordinate system and another are not what we would have expected on the basis of our intuitive ideas. It is very important that we thoroughly understand the relations of space and time implied by the Lorentz transformation.

The Lorentz transformation between the positions and times (x,y,z,t) as measured by an observer “standing still,” and the corresponding coordinates and time (x′,y′,z′,t′) measured inside a “moving” space ship, moving with velocity u are

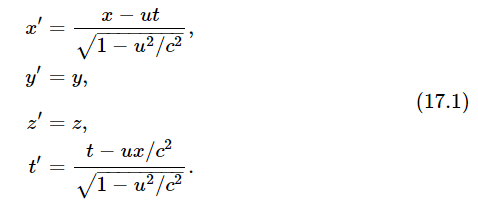
Let us compare these equations with Eq. (11.5), which also relates measurements in two systems, one of which in this instance is rotated relative to the other:

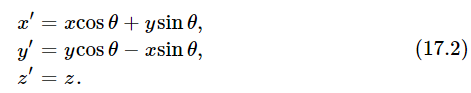
In this particular case, Moe and Joe are measuring with axes having an angle θ between the x′- and x-axes. In each case, we note that the “primed” quantities are “mixtures” of the “unprimed” ones: the new x′ is a mixture of x and y, and the new y′ is also a mixture of x and y.

An analogy is useful: When we look at an object, there is an obvious thing we might call the “apparent width,” and another we might call the “depth.” But the two ideas, width and depth, are not fundamental properties of the object, because if we step aside and look at the same thing from a different angle, we get a different width and a different depth, and we may develop some formulas for computing the new ones from the old ones and the angles involved. Equations (17.2) are these formulas. One might say that a given depth is a kind of “mixture” of all depth and all width. If it were impossible ever to move, and we always saw a given object from the same position, then this whole business would be irrelevant—we would always see the “true” width and the “true” depth, and they would appear to have quite different qualities, because one appears as a subtended optical angle and the other involves some focusing of the eyes or even intuition; they would seem to be very different things and would never get mixed up. It is because we can walk around that we realize that depth and width are, somehow or other, just two different aspects of the same thing.

Can we not look at the Lorentz transformations in the same way? Here also we have a mixture—of positions and the time. A difference between a space measurement and a time measurement produces a new space measurement. In other words, in the space measurements of one man there is mixed in a little bit of the time, as seen by the other. Our analogy permits us to generate this idea: The “reality” of an object that we are looking at is somehow greater (speaking crudely and intuitively) than its “width” and its “depth” because they depend upon how we look at it; when we move to a new position, our brain immediately recalculates the width and the depth. But our brain does not immediately recalculate coordinates and time when we move at high speed, because we have had no effective experience of going nearly as fast as light to appreciate the fact that time and space are also of the same nature. It is as though we were always stuck in the position of having to look at just the width of something, not being able to move our heads appreciably one way or the other; if we could, we understand now, we would see some of the other man’s time—we would see “behind,” so to speak, a little bit.

Thus, we shall try to think of objects in a new kind of world, of space and time mixed together, in the same sense that the objects in our ordinary space-world are real, and can be looked at from different directions. We shall then consider that objects occupying space and lasting for a certain length of time occupy a kind of a “blob” in a new kind of world, and that we look at this “blob” from different points of view when we are moving at different velocities. This new world, this geometrical entity in which the “blobs” exist by occupying position and taking up a certain amount of time, is called space-time. A given point (x,y,z,t) in space-time is called an event. Imagine, for example, that we plot the x-positions horizontally, y and z in two other directions, both mutually at “right angles” and at “right angles” to the paper (!), and time, vertically. Now, how does a moving particle, say, look on such a diagram? If the particle is standing still, then it has a certain x, and as time goes on, it has the same x, the same x, the same x; so, its “path” is a line that runs parallel to the t-axis (Fig. 17–1 a). On the other hand, if it drifts outward, then as the time goes on x increases (Fig. 17–1 b). So, a particle, for example, which starts to drift out and then slows up should have a motion something like that shown in Fig. 17–1(c). A particle, in other words, which is permanent and does not disintegrate is represented by a line in space-time. A particle which disintegrates would be represented by a forked line, because it would turn into two other things which would start from that point.

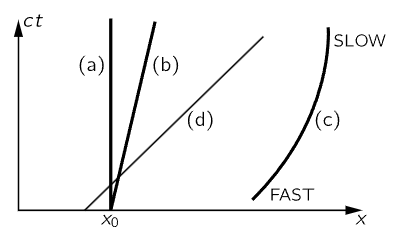
Fig. 17–1. Three particle paths in space-time: (a) a particle at rest at x=x₀; (b) a particle which starts at x=x₀ and moves with constant speed; (c) a particle which starts at high speed but slows down; (d) a light path.

What about light? Light travels at the speed c, and that would be represented by a line having a certain fixed slope (Fig. 17–1 d).

Now according to our new idea, if a given event occurs to a particle, say if it suddenly disintegrates at a certain space-time point into two new ones which follow some new tracks, and this interesting event occurred at a certain value of x and a certain value of t, then we would expect that, if this makes any sense, we just have to take a new pair of axes and turn them, and that will give us the new t and the new x in our new system, as shown in Fig. 17–2(a). But this is wrong, because Eq. (17.1) is not exactly the same mathematical transformation as Eq. (17.2). Note, for example, the difference in sign between the two, and the fact that one is written in terms of cos θ and sin θ, while the other is written with algebraic quantities. (Of course, it is not impossible that the algebraic quantities could be written as cosine and sine, but actually they cannot.) But still, the two expressions are very similar. As we shall see, it is not really possible to think of space-time as a real, ordinary geometry because of that difference in sign. In fact, although we shall not emphasize this point, it turns out that a man who is moving has to use a set of axes which are inclined equally to the light ray, using a special kind of projection parallel to the x′- and t′-axes, for his x′ and t′, as shown in Fig. 17–2(b). We shall not deal with the geometry, since it does not help much; it is easier to work with the equations.

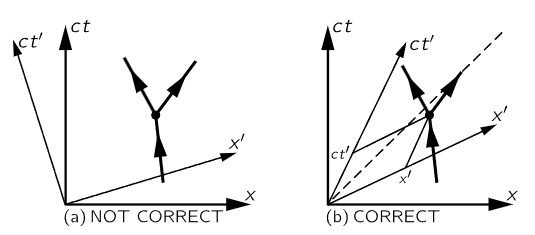
Fig. 17–2. Two views of a disintegrating particle.