General Relativity

The special theory of relativity and its use in the context of classical and quantum mechanics was a revolutionary leap forward in the understanding of a wide variety of physical processes, particularly those involving high energies and speeds. However, it did not fully encompass gravitational phenomena. The problem is that the Newtonian theory of the gravitational force between two bodies presupposes that the force between them is transmitted instantaneously if the mass of one body is increased the other should immediately experience an increase in the attractive force. This implies that the force is being transmitted faster than the speed of light, which is not acceptable. Further, special relativity is only of use in the context of inertial frames of reference: relative motion when one of the frames is accelerating is not taken on board. It was to deal with these problems that in 1915 Einstein formulated what is referred to as the general theory of relativity. It was encompassed in two main postulates. The first was as follows:

1. All the laws of physics can be expressed in such a way that they have the same form in all frames of reference whatever their motion.

Accelerated relative motion of frames of reference is now incorporated, but to achieve this means that the laws have to be expressed in a much more complicated mathematical form. The search still goes on for ways of doing this for all the physical interactions that are known, not least the electromagnetic interaction. The second postulate related to the apparent local equivalence of the gravitational force and acceleration. Everyone has experienced the sensation of increased weight in a lift as it accelerates from rest and goes upwards. The force exerted on the floor of the lift by our bodies increases whilst the lift is accelerating as though the force of gravity due to the earth had increased. The second postulate of general relativity effectively states that in a sufficiently small closed accelerating container, such as a lift, from which there is no opportunity to make an external observation to confirm that it is accelerating, there is no way within the container of determining whether the apparent increase in weight is due to acceleration or to an increase in the force of gravity. The two possible causes of the increase are equivalent. Indeed the second postulate is referred to as the principle of equivalence and can be stated as follows.

2. There is no way for an observer in a sufficiently small closed laboratory to distinguish between the effects of a gravitational force and those produced by accelerated motion.

It is this equivalence that leads to the identity between gravitational and inertial mass mentioned. Clearly, within the general theory of relativity, the gravitational force is treated on a different footing from other types of force. In fact the complex mathematics of general relativity leads to the inescapable conclusion that in the vicinity of matter or energy the nature of space time is modified; it becomes curved or warped. To understand this in terms of our everyday experience is difficult if not impossible, but analogies can help. Imagine a two dimensional being whose only experience of space is motion forwards backwards or left right on a flat surface (see figure 1.1(a)). In this case the shortest distance of travel between two points is a straight line. Introduction of a gravitating body will, according to general relativity, distort the surface as in figure 1.1(b) and the shortest distance of travel on this curved surface is now no longer a straight line. Similarly elementary (Euclidian) geometry, for example Pythagoras’ theorem, no longer holds on this curved surface a triangle is no longer constituted from straight lines. With that analogy in mind the motion of a piece of matter in a gravitational field (e.g. planetary motion) is now interpreted as due to an intrinsic curvature of space and time; a planet in orbit simply moves along the shortest path in curved space time (the equivalent of a straight line in ‘flat’ space time known as a geodesic) and this appears as its orbit in our everyday three dimensional space. It turns out that planetary orbits calculated using general relativity are virtually the same as those calculated using simple classical mechanics and Newton’s form of the gravitational force. However there is one measurable difference for the orbit of Mercury, the planet nearest the sun and, therefore, experiencing the strongest gravitational field. Due to the influence of other planets, its perihelion (the point of its orbit nearest the sun) precesses about

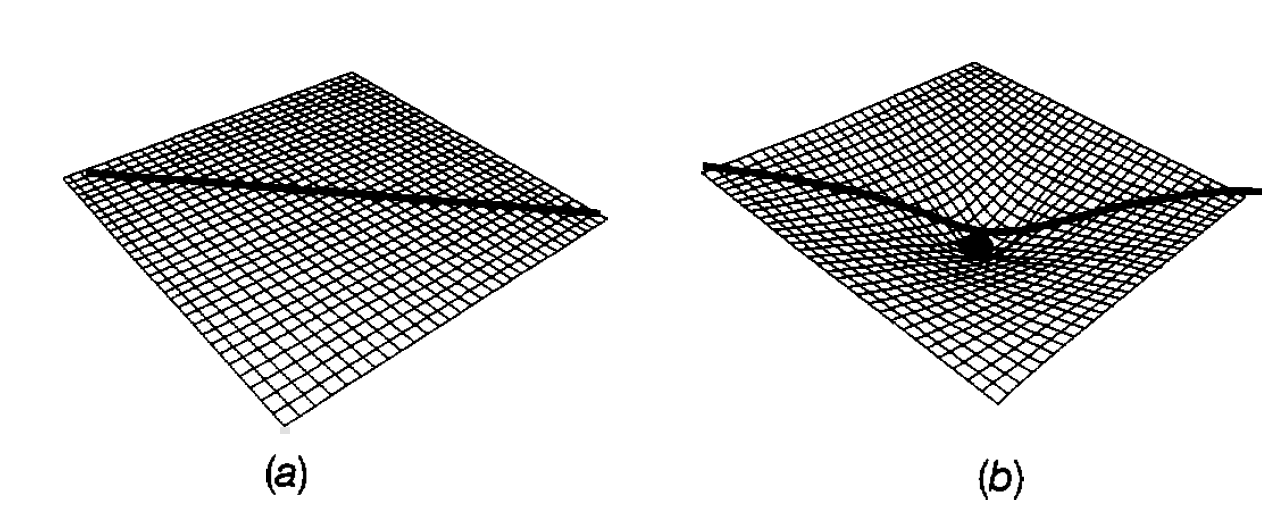
Figure 1.1: Motion on a two dimensional surface (a) when flat and (b) when curved.

the sun as shown in figure 1.2(a). The magnitude of this precession is a little less than 2^o per century, but the measured value is slightly different from the calculated value by somewhat less than one hundredth of a degree per century and it was a tremendous triumph for the general theory of relativity when it was shown that it could account exactly for the discrepancy. The theory made two other testable predictions. One was that due to the curvature of space-time the motion of a light ray passing through a gravitational field should deviate from the usual straight line motion. This is a small effect and can only be tested when the light passes near a very large gravitating body such as the sun. It was checked in 1919 by studying the apparent position of several stars whose light was passing near to the sun (see figure 1.2(b)). Clearly this could only be done during a solar eclipse otherwise the light from the sun overwhelms that from the star. It was found that the apparent position of such a star did indeed differ from its observed position at other times when its light did not pass near the sun and that the measured deviation agreed well with the theoretical prediction. Another prediction was that, because of the curvature of space time, the rate of a clock in a high gravitational field is slightly slower than when in smaller gravitational field. This is an

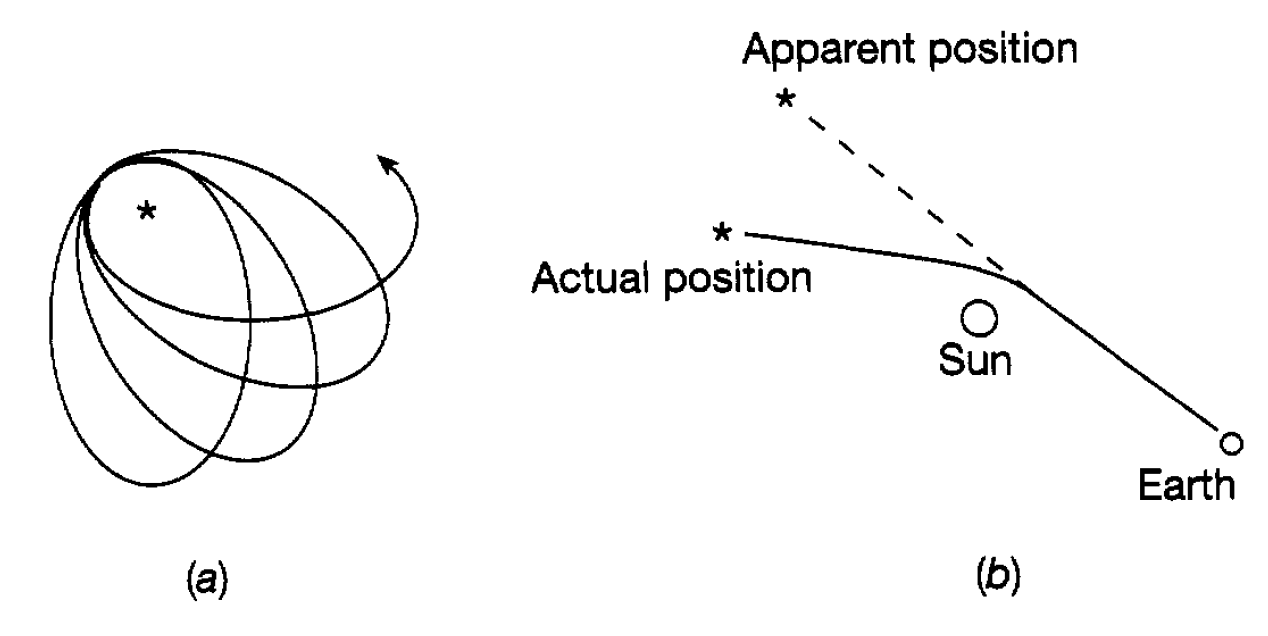
Figure 1.2: (a) The precession of the perihelion of Mercury. (b) The curved path of a light ray near the sun.

additional form of time dilation to that due to motion in the context of special relativity. Clocks should run more slowly on the surface of the earth than up in the atmosphere or in outer space. The effect is very small of the order 1 part in the unit of time is the time taken for one vibration of the electromagnetic radiation emitted by an atom usually caesium) carried on ‘round the world’ journeys during 1971-2 by a commercial airliner at high altitude (around 10,000 m). To check the theory it was also necessary to take into account the special relativity time dilation resulting from the airliner’s motion. Other checks have been made more recently using measurements in a spacecraft and also by studying the frequency of light from atoms at the surface of the sun, where there is a strong gravitational field, compared with that of light emitted by identical atoms on the earth where the gravitational field is much weaker. A final prediction was that moving objects, especially heavy ones, would cause ripples in space time analogous to a moving object making ripples in a pond. These ripples are referred to as gravitational waves and they are rather like electromagnetic waves produced by moving electric charges. This effect would lead to a moving body losing energy by gravitational radiation. However the effect is very small indeed and, so far, no gravitational waves have been detected. However, the resultant energy loss has been measured in rotating pairs of neutron stars. Here it should also be noted that the quantized version of this gravitational radiation, possibly equivalent to the photons associated with electromagnetic radiation, and known as gravitons, enter theories incorporating all the elementary particle interactions, but, unlike photons which have spin 1, gravitons have spin 2. One interesting feature of the general theory of relativity is that, as first formulated by Einstein, it predicts that the universe is in a state of continual expansion. As will be indeed, seem to be the case. However in Einstein’s time it was believed that the universe was static. For that reason he introduced a constant, known as the cosmological constant, into the theory; this effectively cancelled the expansion. Since the general theory does allow the presence of such a constant and since the universe is expanding, its precise value is now subject to much discussion.