


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2021
Date: 27-12-2021
Date: 14-2-2017
|
The product of a family 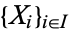 of objects of a category is an object
of objects of a category is an object 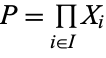 , together with a family of morphisms
, together with a family of morphisms 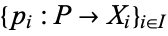 such that for every object
such that for every object  and every family of morphisms
and every family of morphisms 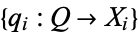 there is a unique morphism
there is a unique morphism 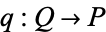 such that
such that
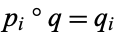 |
for all 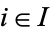 . The product is unique up to isomorphisms.
. The product is unique up to isomorphisms.
In the category of sets, the product is the Cartesian product, and in the category of groups it is the group direct product. In both cases, 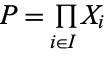 , and
, and 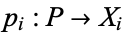 is the projection onto the
is the projection onto the 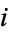 th factor.
th factor.
REFERENCES:
Joshi, K. D. "Products and Coproducts." Ch. 8 in Introduction to General Topology. New Delhi, India: Wiley, pp. 189-216, 1983.
Kasch, F. "Construction of Products and Coproducts." §4.80 in Modules and Rings. New York: Academic Press, pp. 80-84, 1982.
Rowen, L. "Products and Coproducts." In Ring Theory, Vol. 1. San Diego, CA: Academic Press, pp. 73-76, 1988.
Strooker, J. R. "Products and Sums." §1.5 in Introduction to Categories, Homological Algebra and Sheaf Cohomology Cambridge, England: Cambridge University Press, pp. 14-21, 1978.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تدعو جامعة الكرخ للمشاركة في الحفل المركزي لتخرج طلبة الجامعات
|
|
|