


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-12-2021
Date: 16-1-2022
Date: 11-1-2022
|
In common usage, an ordinal number is an adjective which describes the numerical position of an object, e.g., first, second, third, etc.
In formal set theory, an ordinal number (sometimes simply called an "ordinal" for short) is one of the numbers in Georg Cantor's extension of the whole numbers. An ordinal number is defined as the order type of a well ordered set (Dauben 1990, p. 199; Moore 1982, p. 52; Suppes 1972, p. 129). Finite ordinal numbers are commonly denoted using arabic numerals, while transfinite ordinals are denoted using lower case Greek letters.
It is easy to see that every finite totally ordered set is well ordered. Any two totally ordered sets with 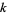 elements (for
elements (for 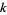 a nonnegative integer) are order isomorphic, and therefore have the same order type (which is also an ordinal number). The ordinals for finite sets are denoted 0, 1, 2, 3, ..., i.e., the integers one less than the corresponding nonnegative integers.
a nonnegative integer) are order isomorphic, and therefore have the same order type (which is also an ordinal number). The ordinals for finite sets are denoted 0, 1, 2, 3, ..., i.e., the integers one less than the corresponding nonnegative integers.
The first transfinite ordinal, denoted  , is the order type of the set of nonnegative integers (Dauben 1990, p. 152; Moore 1982, p. viii; Rubin 1967, pp. 86 and 177; Suppes 1972, p. 128). This is the "smallest" of Cantor's transfinite numbers, defined to be the smallest ordinal number greater than the ordinal number of the whole numbers. Conway and Guy (1996) denote it with the notation
, is the order type of the set of nonnegative integers (Dauben 1990, p. 152; Moore 1982, p. viii; Rubin 1967, pp. 86 and 177; Suppes 1972, p. 128). This is the "smallest" of Cantor's transfinite numbers, defined to be the smallest ordinal number greater than the ordinal number of the whole numbers. Conway and Guy (1996) denote it with the notation 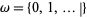 .
.
From the definition of ordinal comparison, it follows that the ordinal numbers are a well ordered set. In order of increasing size, the ordinal numbers are 0, 1, 2, ..., 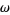 ,
, 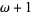 ,
, 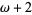 , ...,
, ..., 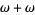 ,
, 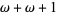 , .... The notation of ordinal numbers can be a bit counterintuitive, e.g., even though
, .... The notation of ordinal numbers can be a bit counterintuitive, e.g., even though 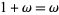 ,
, 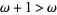 . The cardinal number of the set of countable ordinal numbers is denoted
. The cardinal number of the set of countable ordinal numbers is denoted 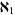 (aleph-1).
(aleph-1).
If 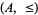 is a well ordered set with ordinal number
is a well ordered set with ordinal number 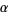 , then the set of all ordinals
, then the set of all ordinals 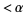 is order isomorphic to
is order isomorphic to 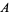 . This provides the motivation to define an ordinal as the set of all ordinals less than itself. John von Neumann defined a set
. This provides the motivation to define an ordinal as the set of all ordinals less than itself. John von Neumann defined a set 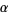 to be an ordinal number iff
to be an ordinal number iff
1. If 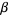 is a member of
is a member of 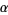 , then
, then 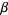 is a proper subset of
is a proper subset of 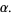
2. If 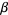 and
and 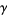 are members of
are members of 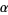 then one of the following is true:
then one of the following is true: 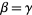 ,
, 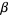 is a member of
is a member of 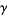 , or
, or 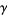 is a member of
is a member of 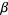 .
.
3. If 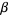 is a nonempty proper subset of
is a nonempty proper subset of 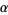 , then there exists a
, then there exists a 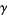 member of
member of 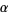 such that the intersection
such that the intersection 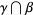 is empty.
is empty.
(Rubin 1967, p. 176; Ciesielski 1997, p. 44). This is the standard representation of ordinals. In this representation,
| symbol | elements | description |
| 0 | 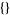 |
empty set |
| 1 | 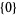 |
set of one element |
| 2 | 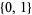 |
set of two elements |
| 3 | 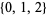 |
set of three elements |
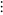 |
||
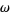 |
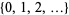 |
set of all finite ordinals |
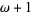 |
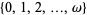 |
|
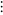 |
||
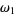 |
set of all countable ordinals | |
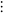 |
||
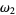 |
set of all countable and 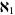 ordinals ordinals |
|
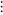 |
||
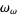 |
set all finite ordinals and 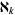 ordinals for all nonnegative integers ordinals for all nonnegative integers 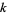 |
|
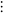 |
Rubin (1967, p. 272) provides a nice definition of the 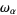 ordinals.
ordinals.
Since for any ordinal 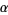 , the union
, the union 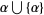 is a bigger ordinal
is a bigger ordinal 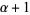 , there is no largest ordinal, and the class of all ordinals is therefore a proper class (as shown by the Burali-Forti paradox).
, there is no largest ordinal, and the class of all ordinals is therefore a proper class (as shown by the Burali-Forti paradox).
Ordinal numbers have some other rather peculiar properties. The sum of two ordinal numbers can take on two different values, the sum of three can take on five values. The first few terms of this sequence are 2, 5, 13, 33, 81, 193, 449, 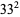 ,
, 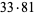 ,
, 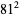 ,
, 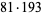 ,
, 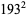 , ..., namely 2, 5, 13, 33, 81, 193, 449, 1089, 2673, 6561, 15633, 37249, ... (Conway and Guy 1996, OEIS A005348). The sum of
, ..., namely 2, 5, 13, 33, 81, 193, 449, 1089, 2673, 6561, 15633, 37249, ... (Conway and Guy 1996, OEIS A005348). The sum of 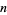 ordinals has either
ordinals has either 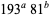 or
or 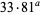 possible answers for
possible answers for 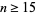 (Conway and Guy 1996).
(Conway and Guy 1996).
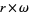 is the same as
is the same as 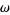 , but
, but 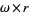 is equal to
is equal to 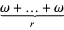 .
. 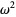 is larger than any number of the form
is larger than any number of the form 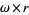 ,
, 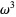 is larger than
is larger than 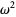 , and so on.
, and so on.
There exist ordinal numbers which cannot be constructed from smaller ones by finite additions, multiplications, and exponentiations. These ordinals obey Cantor's equation. The first such ordinal is
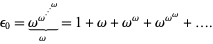 |
The next is
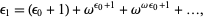 |
then follow 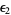 ,
, 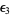 , ...,
, ..., 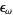 ,
, 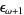 , ...,
, ..., 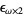 , ...,
, ..., 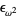 ,
, 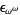 , ...,
, ..., 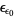 ,
, 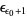 , ...,
, ..., 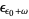 , ...,
, ..., 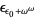 , ...,
, ..., 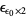 , ...,
, ..., 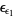 , ...,
, ..., 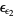 , ...,
, ..., 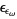 , ...,
, ..., 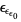 , ...,
, ..., 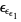 , ...,
, ..., 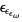 , ...,
, ..., 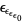 , ... (Conway and Guy 1996).
, ... (Conway and Guy 1996).
Ordinal addition, ordinal multiplication, and ordinal exponentiation can all be defined. Although these definitions also work perfectly well for order types, this does not seem to be commonly done. There are two methods commonly used to define operations on the ordinals: one is using sets, and the other is inductively.
REFERENCES:
Cantor, G. Über unendliche, lineare Punktmannigfältigkeiten, Arbeiten zur Mengenlehre aus dem Jahren 1872-1884. Leipzig, Germany: Teubner-Archiv zur Mathematik, 1884.
Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.
Conway, J. H. and Guy, R. K. "Cantor's Ordinal Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 266-267 and 274, 1996.
Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.
Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.
Sloane, N. J. A. Sequence A005348/M1435 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|