


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2021
Date: 24-11-2021
Date: 18-11-2021
|
A tetraview is a visualization technique for bivariate complex functions. In the simplest case, the graph of a complex-valued function 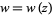 can be considered as a hypersurface in
can be considered as a hypersurface in 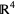 with four real coordinates
with four real coordinates ![(R[z],I[z],R[w(z)],I[w(z)])](https://mathworld.wolfram.com/images/equations/Tetraview/Inline3.gif) . Carrying out a rotation in four dimensions and projecting the first three coordinates into (ordinary)
. Carrying out a rotation in four dimensions and projecting the first three coordinates into (ordinary) 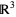 then allows the changes from
then allows the changes from ![(R[z],I[z],R[w(z)])](https://mathworld.wolfram.com/images/equations/Tetraview/Inline5.gif) to
to ![(R[z],I[z],I[w(z)])](https://mathworld.wolfram.com/images/equations/Tetraview/Inline6.gif) to
to ![(R[w(z)],I[w(z)],R[z])](https://mathworld.wolfram.com/images/equations/Tetraview/Inline7.gif) to
to ![(R[w(z)],I[w(z)],I[z])](https://mathworld.wolfram.com/images/equations/Tetraview/Inline8.gif) to be visualized continuously.
to be visualized continuously.
REFERENCES:
Banchoff, T. "Surfaces Beyond the Third Dimension." http://www.math.brown.edu/~banchoff/art/PAC-9603/tour/wall-1a.html.
Banchoff, T. "The Mathematics of the Tetraview." http://www.math.brown.edu/~banchoff/art/PAC-9603/tour/tetra-Z2/tetra-math.html.
Banchoff, T. "A Virtual Reconstruction of a Virtual Exhibit." In Multimedia Tools for Communicating Mathematics. Papers from the International Workshop Held at the University of Lisbon, Lisbon, November 2000 (Ed. J. Borwein, M. H. Morales, K. Polthier, and J. F. Rodrigues). Berlin: Springer-Verlag, Berlin, pp. 29-38, 2002.
Banchoff, T. F. "Computer Graphics in Mathematical Research, from ICM 1978 to ICM 2002: A Personal Reflection." In Proceedings of the 1st International Conference held in Beijing, August 17-19, 2002 (Ed. A. M. Cohen, X.-S. Gao, and N. Takayama). Singapore: World Scientific, pp. 180-189, 2002.
Banchoff, T. and Cervone, D. P. "Understanding Complex Function Graphs." Commun. Visual Math. 1, July 1998. http://www.math.union.edu/~dpvc/CVM-07-98/1998/01/ucfg/.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|