


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-9-2021
Date: 21-9-2021
Date: 16-12-2021
|
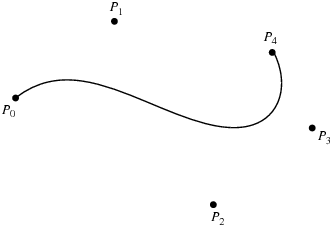
Given a set of 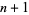 control points
control points 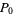 ,
, 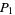 , ...,
, ..., 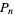 , the corresponding Bézier curve (or Bernstein-Bézier curve) is given by
, the corresponding Bézier curve (or Bernstein-Bézier curve) is given by
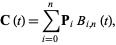 |
where 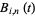 is a Bernstein polynomial and
is a Bernstein polynomial and ![t in [0,1]](https://mathworld.wolfram.com/images/equations/BezierCurve/Inline6.gif) . Bézier splines are implemented in the Wolfram Language as BezierCurve[pts].
. Bézier splines are implemented in the Wolfram Language as BezierCurve[pts].
A "rational" Bézier curve is defined by
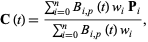 |
where 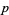 is the order,
is the order, 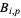 are the Bernstein polynomials,
are the Bernstein polynomials, 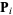 are control points, and the weight
are control points, and the weight 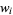 of
of 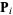 is the last ordinate of the homogeneous point
is the last ordinate of the homogeneous point 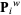 . These curves are closed under perspective transformations, and can represent conic sections exactly.
. These curves are closed under perspective transformations, and can represent conic sections exactly.
The Bézier curve always passes through the first and last control points and lies within the convex hull of the control points. The curve is tangent to 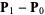 and
and 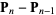 at the endpoints. The "variation diminishing property" of these curves is that no line can have more intersections with a Bézier curve than with the curve obtained by joining consecutive points with straight line segments. A desirable property of these curves is that the curve can be translated and rotated by performing these operations on the control points.
at the endpoints. The "variation diminishing property" of these curves is that no line can have more intersections with a Bézier curve than with the curve obtained by joining consecutive points with straight line segments. A desirable property of these curves is that the curve can be translated and rotated by performing these operations on the control points.
Undesirable properties of Bézier curves are their numerical instability for large numbers of control points, and the fact that moving a single control point changes the global shape of the curve. The former is sometimes avoided by smoothly patching together low-order Bézier curves. A generalization of the Bézier curve is the B-spline.
REFERENCES:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. "Bézier Curves." Ch. 10 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, pp. 211-245, 1998.
Piegl, L. Fundamental Developments of Computer Aided Geometric Design. San Diego, CA: Academic Press, 1993.
Shene, C.-K. "Introduction to Computing with Geometry Notes. Unit 5: Bézier Curves." http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|