Random Closed Set

A random closed set (RACS) in 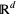 is a measurable function from a probability space  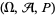into 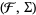 where 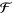 is the collection of all closed subsets of  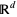and where  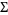denotes the sigma-algebra generated over  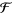the by sets

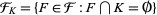for all compact subsets .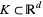

Originally, RACS were defined not on 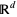 but in the more general setting of locally compact and separable (LCS) topological spaces (Baudin 1984) which may or may not be T2. In this case, the above definition is modified so that  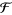is defined to be the collection of closed subsets of some ambient LCS space  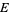(Molchanov 2005).

Despite a number of apparent differences, one can show that multidimensional point processes are a special case of RACS when talking about 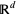 (Baudin 1984).

REFERENCES:

Baudin, M. "Multidimensional Point Processes and Random Closed Sets." J. Appl. Prob. 21, 173-178, 1984.

Matheron, G. Random Sets and Integral Geometry. New York: Wiley, 1975.

Molchanov, I. "Random Closed Sets." In Space, Structure and Randomness: Contributions in Honor of Georges Matheron in the Fields of Geostatistics, Random Sets and Mathematical Morphology. New York: Springer Science+Business Media, 2005.