


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 16-7-2017
Date: 18-5-2016
Date: 24-10-2020
|
A mass on a vertical spring
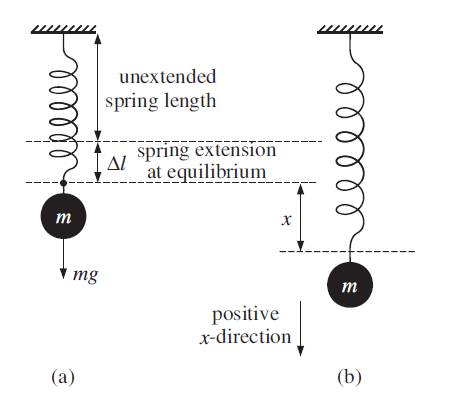
Figure 1.1 An oscillating mass on a vertical spring. (a) The mass at its equilibrium position. (b) The mass displaced by a distance x from its equilibrium position.
If we suspend a mass from a vertical spring, as shown in Figure 1.1, we have gravity also acting on the mass. When the mass is initially attached to the spring, the length of the spring increases by an amount Δl. Taking displacements in the downward direction as positive, the resultant force on the mass is equal to the gravitational force minus the force exerted upwards by the spring, i.e. the resultant force is given by mg − kΔl. The resultant force is equal to zero when the mass is at its equilibrium position. Hence
kΔl = mg.
When the mass is displaced downwards by an amount x, the resultant force is given by
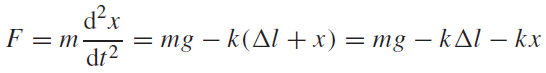
i.e.
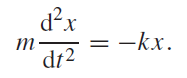
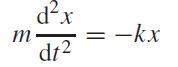 ..........(1)
..........(1)
Perhaps not surprisingly, this result is identical to the equation of motion (1) of the horizontal spring: we simply need to measure displacements from the equilibrium position of the mass.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|