Fermat's Polygonal Number Theorem

In 1638, Fermat proposed that every positive integer is a sum of at most three triangular numbers, four square numbers, five pentagonal numbers, and 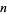 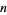-polygonal numbers. Fermat claimed to have a proof of this result, although Fermat's proof has never been found. Gauss proved the triangular case, and noted the event in his diary on July 10, 1796, with the notation

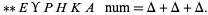This case is equivalent to the statement that every number of the form 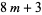 is a sum of three odd squares (Duke 1997). More specifically, a number is a sum of three squares iff it is not of the form  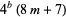for 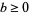, as first proved by Legendre in 1798.

Euler was unable to prove the square case of Fermat's theorem, but he left partial results which were subsequently used by Lagrange. The square case was finally proved by Jacobi and independently by Lagrange in 1772. It is therefore sometimes known as Lagrange's four-square theorem. In 1813, Cauchy proved the proposition in its entirety.

REFERENCES:

Cassels, J. W. S. Rational Quadratic Forms. New York: Academic Press, 1978.

Cauchy, A. "Démonstration du théorème général de Fermat sur les nombres polygones." In Oeuvres complètes d'Augustin Cauchy, Vol. VI (II Série). Paris: Gauthier-Villars, pp. 320-353, 1905.

Conway, J. H.; Guy, R. K.; Schneeberger, W. A.; and Sloane, N. J. A. "The Primary Pretenders." Acta Arith. 78, 307-313, 1997.

Duke, W. "Some Old Problems and New Results about Quadratic Forms." Not. Amer. Math. Soc. 44, 190-196, 1997.

Nathanson, M. B. "A Short Proof of Cauchy's Polygonal Number Theorem." Proc. Amer. Math. Soc. 9, 22-24, 1987.

Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 143-144, 1993.

Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 91, 1984.