


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2019
Date: 26-7-2019
Date: 22-5-2019
|
If, for 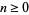 ,
,
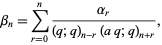 |
(1) |
then
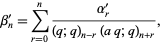 |
(2) |
where
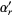 |
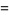 |
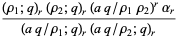 |
(3) |
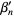 |
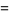 |
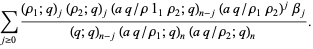 |
(4) |
REFERENCES:
Andrews, G. E. "Multiple Series Rogers-Ramanujan Type Identities." Pacific J. Math. 114, 267-283, 1984.
Andrews, G. E. "Bailey's Lemma" and "Bailey's Lemma in Computer Algebra." §3.4 and 10.4 in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 25-27 and 99-100, 1986.
Andrews, G. E. "The Fifth and Seventh Order Mock Theta Functions." Trans. Amer. Soc. 293, 113-134, 1986.
Andrews, G. E. "Mock Theta Functions." Proc. Sympos. Pure Math. 49, 283-298, 1989.
Andrews, G. E. and Hickerson, D. "Ramanujan's 'Lost' Notebook VII: The Sixth Order Mock Theta Functions." Adv. Math. 89, 60-105, 1991.
Bailey, W. N. "Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. 50, 1-10, 1949.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|