


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2018
Date: 18-8-2018
Date: 20-8-2018
|
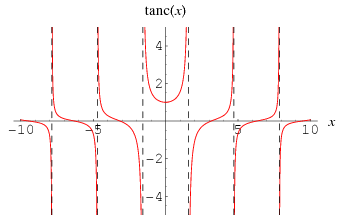
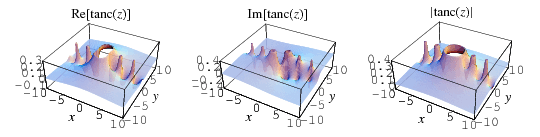
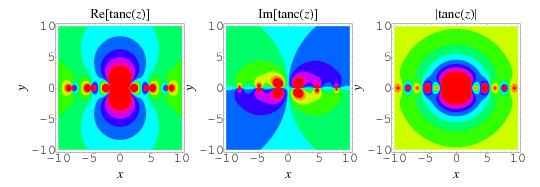
By analogy with the sinc function, define the tanc function by
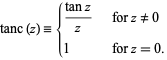 |
(1) |
Since 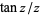 is not a cardinal function, the "analogy" with the sinc function is one of functional structure, not mathematical properties. It is quite possible that a better term than
is not a cardinal function, the "analogy" with the sinc function is one of functional structure, not mathematical properties. It is quite possible that a better term than 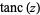 , as introduced here, could be coined, although there appears to be no name previously assigned to this function.
, as introduced here, could be coined, although there appears to be no name previously assigned to this function.
The derivative is given by
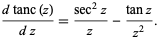 |
(2) |
The indefinite integral can apparently not be done in closed form in terms of conventionally defined functions.
This function commonly arises in problems in physics, where it is desired to determine values of  for which
for which 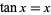 , i.e.,
, i.e., 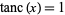 . This is a transcendental equation whose first few solutions are given in the following table and illustrated above.
. This is a transcendental equation whose first few solutions are given in the following table and illustrated above.
 |
OEIS | root |
| 0 | 0 | |
| 1 | A115365 | 4.4934094579090641753... |
| 2 | 7.7252518369377071642... | |
| 3 | 10.904121659428899827... | |
| 4 | 14.066193912831473480... | |
| 5 | 17.220755271930768739... |
The positive solutions can be written explicitly in series form as
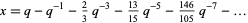 |
(3) |
(OEIS A079330 and A088989), where the series in 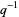 can be found by series reversion of the series for
can be found by series reversion of the series for 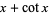 and
and
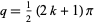 |
(4) |
for 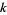 a positive integer (D. W. Cantrell, pers. comm., Jan. 3, 2003). In practice, the first three terms of the series often suffice for obtaining approximate solutions.
a positive integer (D. W. Cantrell, pers. comm., Jan. 3, 2003). In practice, the first three terms of the series often suffice for obtaining approximate solutions.
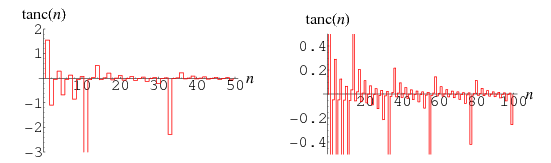
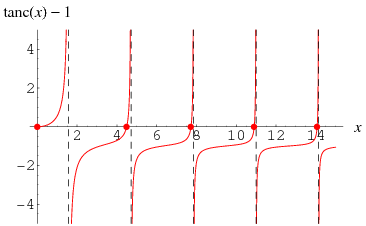
Because of the vertical asymptotes of 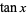 as odd multiples of
as odd multiples of 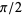 , this function is much less well-behaved than the sinc function, even as
, this function is much less well-behaved than the sinc function, even as 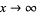 . The plot above shows
. The plot above shows 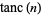 for integers
for integers  . The values of
. The values of  giving incrementally smallest values of
giving incrementally smallest values of  are
are 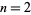 , 11, 1317811389848379909481978463177998812826691414678853402757616, ...(OEIS A079331), corresponding to values of
, 11, 1317811389848379909481978463177998812826691414678853402757616, ...(OEIS A079331), corresponding to values of 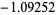 ,
, 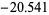 ,
, 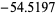 ,
, 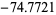 , .... Similarly, the values of
, .... Similarly, the values of 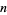 giving incrementally largest values of
giving incrementally largest values of 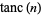 are
are 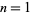 , 122925461, 534483448, 3083975227, 214112296674652, ... (OEIS A079332), corresponding to 1.55741, 2.65934, 3.58205, 4.3311, 18.0078, 18.0566, 556.306, ... (D. W. Cantrell, pers. comm., Jan. 3, 2002). The following table (P. Carmody, pers. comm., Nov. 21, 2003) extends these results up through the 194,000 term of the continued fraction. All these extrema correspond to numerators of the continued fraction expansion of
, 122925461, 534483448, 3083975227, 214112296674652, ... (OEIS A079332), corresponding to 1.55741, 2.65934, 3.58205, 4.3311, 18.0078, 18.0566, 556.306, ... (D. W. Cantrell, pers. comm., Jan. 3, 2002). The following table (P. Carmody, pers. comm., Nov. 21, 2003) extends these results up through the 194,000 term of the continued fraction. All these extrema correspond to numerators of the continued fraction expansion of 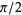 . In addition, since they must be near an odd multiple of
. In addition, since they must be near an odd multiple of 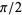 in order for
in order for 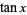 to be large, the corresponding denominators must be odd. There is also a very strong correlation between
to be large, the corresponding denominators must be odd. There is also a very strong correlation between 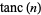 and the value of the subsequent term in the continued fraction expansion (i.e., a high value there implies the prior convergent was a good approximation to
and the value of the subsequent term in the continued fraction expansion (i.e., a high value there implies the prior convergent was a good approximation to 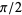 ).
).
| smallest | convergent | largest |
| 1 | 1.55741 | |
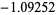 |
2 | |
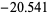 |
4 | |
| 15 | 2.659341 | |
| 17 | 3.582052 | |
| 19 | 4.331096 | |
| 29 | 18.007800 | |
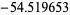 |
118 | |
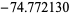 |
136 | |
| 233 | 18.056613 | |
| 315 | 556.306227 | |
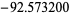 |
1134 | |
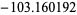 |
1568 | |
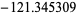 |
1718 | |
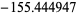 |
2154 | |
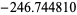 |
2468 | |
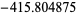 |
3230 | |
| 3727 | 2750.202396 | |
| 3763 | 10539.847388 | |
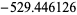 |
5187 | |
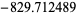 |
8872 | |
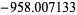 |
9768 | |
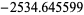 |
11282 | |
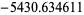 |
12284 | |
| 15503 | 24263.751532 | |
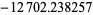 |
24604 | |
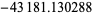 |
153396 | |
| 156559 | 228085.415076 |
The sequences of maxima and minima are almost certainly unbounded, but it is not known how to prove this fact.
REFERENCES:
Sloane, N. J. A. Sequences A079330, A088989, and A115365 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|