


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-11-2018
Date: 28-10-2018
Date: 18-10-2018
|
A branch point of an analytic function is a point in the complex plane whose complex argument can be mapped from a single point in the domain to multiple points in the range. For example, consider the behavior of the point 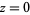 under the power function
under the power function
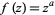 |
(1) |
for complex non-integer 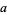 , i.e.,
, i.e., 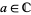 with
with 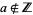 . Writing
. Writing 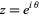 and taking
and taking 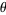 from 0 to
from 0 to 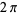 gives
gives
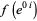 |
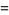 |
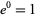 |
(2) |
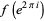 |
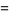 |
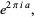 |
(3) |
so the values of 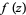 at
at 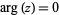 and
and 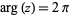 are different, despite the fact that they correspond to the same point in the domain.
are different, despite the fact that they correspond to the same point in the domain.
Branch points whose neighborhood of values wrap around the range a finite number of times 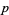 as
as 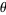 varies from 0 to
varies from 0 to 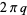 correspond to the point
correspond to the point 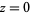 under functions of the form
under functions of the form 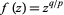 and are called algebraic branch points of order
and are called algebraic branch points of order 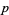 . A branch point whose neighborhood of values wraps around an infinite number of times occurs at the point
. A branch point whose neighborhood of values wraps around an infinite number of times occurs at the point 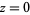 under the function
under the function 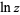 and is called a logarithmic branch point. Logarithmic branch points are equivalent to logarithmic singularities.
and is called a logarithmic branch point. Logarithmic branch points are equivalent to logarithmic singularities.
Pinch points are also called branch points.
It should be noted that the endpoints of branch cuts are not necessarily branch points.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 397-399, 1985.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 391-392 and 399-401, 1953.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 188-191, 2004. http://www.mathematicaguidebooks.org/.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|