


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2018
Date: 28-11-2018
Date: 28-11-2018
|
An entire function which is a generalization of the Bessel function of the first kind defined by
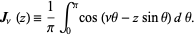 |
Anger's original function had an upper limit of 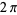 , but the current notation was standardized by Watson (1966).
, but the current notation was standardized by Watson (1966).
The Anger function may also be written as
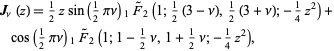 |
where 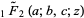 is a regularized hypergeometric function.
is a regularized hypergeometric function.
If  is an integer
is an integer 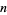 , then
, then 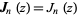 , where
, where 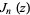 is a Bessel function of the first kind.
is a Bessel function of the first kind.
The Anger function is implemented in the Wolfram Language as AngerJ[nu, z].
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Anger and Weber Functions." §12.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 498-499, 1972.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Anger Function 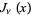 and Weber Function
and Weber Function 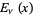 ." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|