


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-8-2019
Date: 25-4-2019
Date: 22-4-2019
|
A number defined by 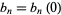 , where
, where 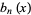 is a Bernoulli polynomial of the second kind (Roman 1984, p. 294), also called Cauchy numbers of the first kind. The first few for
is a Bernoulli polynomial of the second kind (Roman 1984, p. 294), also called Cauchy numbers of the first kind. The first few for 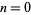 , 1, 2, ... are 1, 1/2,
, 1, 2, ... are 1, 1/2, 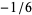 , 1/4,
, 1/4, 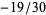 , 9/4, ... (OEIS A006232 and A006233). They are given by
, 9/4, ... (OEIS A006232 and A006233). They are given by
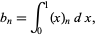 |
where 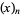 is a falling factorial, and have exponential generating function
is a falling factorial, and have exponential generating function
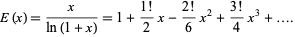 |
REFERENCES:
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 294, 1974.
Jeffreys, H. and Jeffreys, B. S. Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 259, 1988.
Roman, S. The Umbral Calculus. New York: Academic Press, p. 114, 1984.
Sloane, N. J. A. Sequences A006232/M5067 and A006233/M1558 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|