


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-9-2018
Date: 23-5-2019
Date: 5-9-2019
|
An elliptic function can be characterized by its real and imaginary half-periods 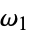 and
and 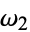 (Whittaker and Watson 1990, p. 428), sometimes also denoted
(Whittaker and Watson 1990, p. 428), sometimes also denoted 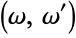 (Abramowitz and Stegun 1972, p. 630). The Wolfram Languagecommand WeierstrassHalfPeriods[
(Abramowitz and Stegun 1972, p. 630). The Wolfram Languagecommand WeierstrassHalfPeriods[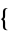 g2, g3
g2, g3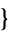 ] gives the half-periods
] gives the half-periods 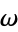 and
and 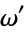 corresponding to the invariants
corresponding to the invariants 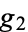 and
and 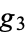 for a Weierstrass elliptic function.
for a Weierstrass elliptic function.
The notation
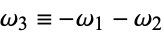 |
(1) |
is sometimes also defined (Whittaker and Watson 1990, p. 443), although Abramowitz and Stegun (1972, p. 630) instead use the definition
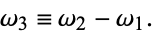 |
(2) |
In the case of a Weierstrass elliptic function, consider the modular discriminant
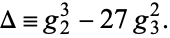 |
(3) |
If 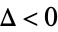 , then
, then 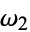 is real, and
is real, and 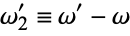 is pure imaginary. However, if
is pure imaginary. However, if 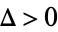 , then
, then 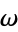 is real and
is real and 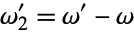 is pure imaginary.
is pure imaginary.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 630, 1972.
Brezhnev, Y. V. "Uniformisation: On the Burnside Curve 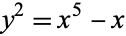 ." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.
." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|