It can hardly be overstressed how useful the concept of a point mass is in Newtonian mechanics and gravity. It allows us to probe the gravitational field pointwise and to reduce the dynamical problem to the mathematical problem of finding solutions to a system of finitely many ordinary differential equations. To be sure, just postulating the existence of point masses is not sufficient. To be consistent with the known laws of physics, one must eventually understand the point mass as an idealization of a highly localized mass distribution which obeys known field-theoretic laws, such that in the situations at hand most of the field degrees of freedom effectively decouple from the dynamical laws for those collective degrees of freedom in which one is interested, e.g. the centre of mass.

In Newtonian gravity this usually requires clever approximation schemes but is not considered to be a problem of fundamental nature. Although this is true for the specific linear theory of Newtonian gravity, this need not be so for comparably simple generalizations, as will become clear later. In GR the situation is markedly different. A concentration of more than one Schwarzschild mass in a region of radius less than the Schwarzschild radius will lead to a black hole whose behaviour away from the stationary state cannot usually be well described by finitely many degrees of freedom. It shakes and vibrates, thereby radiating off energy and angular momentum in the form of gravitational radiation. Moreover, it is an extended object and cannot be unambiguously ascribed an (absolute or relative) position or individual mass. Hence the problem of motion, and therefore the problem of scattering of black holes, cannot be expected to merely consist of corrections to Newtonian scattering problems. Rather, the whole kinematic and dynamical setup will be different where many of the established concepts of Newtonian physics need to be replaced or at least adapted, very often in a somewhat ambiguous way. Among these  are mass, distance, and kinetic energy. For example, one may try to solve the following straightforward sounding problem in GR, whose solution one might think has been given long ago. Consider two unspinning black holes, momentarily at rest, with equal individual mass m, mutual distance ℓ, and no initial gravitational radiation around. What is the amount of energy released via gravitational radiation during the dynamical infall? In such a situation we can usually make sense of the notions of ‘spin’ (hence unspinning) and ‘mass’; but ambiguities generally exist in defining ‘distance’ and, most important of all, ‘initial gravitational radiation’. Such difficulties persist over and above the ubiquitous analytical and/or numerical problems which are currently under attack by many research groups.

To those who are not so familiar with GR and like to see Newtonian analogies, I wish to mention that there is a way to consistently model some of the nonlinear features of Einstein’s equations in a Newtonian context, which shares the property that it does not allow for point masses. I will briefly describe this model since it does not seem to be widely known.

First recall the field equation in Newtonian gravity, which allows us to determine the gravitational potential φ (whose negative gradient, -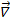 φ, is the gravitational field) from the mass density ρ (the ‘source’ of the gravitational field):

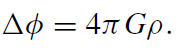 (1.1)

Now suppose one imposes the following principle for a modification of (1.1): all energies, including the self-energy of the gravitational field, act as source for the gravitational field. In order to convert an energy density Ɛ into a mass density ρ, we adopt the relation Ɛ = ρc² from special relativity (the equation we will arrive at can easily be made Lorentz invariant by adding appropriate time derivatives). The question then is whether one can modify the source term of (1.1) such that ρ → ρ + ρ_grav with ρ_grav := ε_grav/c², where Ɛ_grav is the energy density of the gravitational field as predicted by this very same equation (condition of self-consistency).

It turns out that there is indeed a unique such modification, which reads:

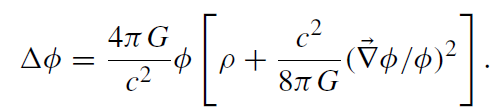 (1.2)

It is shown in the appendix at the end of the chapter that this equation indeed satisfies the ‘energy principle’ as just stated. (For more information and a proof of uniqueness). The gravitational potential is now required to be always positive, tending to the value c² at spatial infinity (rather than zero as for (1.1)). The second term on the right-hand side of (1.2) corresponds to the energy density of the gravitational field. Unlike the energy density following from (1.1) (which is -1/8πG |∇φ|²) it is now positive definite. This does not contradict the attracttivity of gravity for the following reason: the rest-energy density of a piece of matter is in this theory not given by ρc², but by ρφ, that is, it depends on the value of the gravitational potential at the location of the matter. The same piece of matter located at a lower gravitational potential has less energy than at higher potential values. In GR this is called the universal redshift effect. Here, as in GR, the active gravitational mass also suffers from this redshift, as is immediate from the first term on the right-hand side of (1.2), where ρ does not enter alone, as in (1.1), but is multiplied with the gravitational potential φ. With respect to these features our modification (1.2) of Newtonian gravity mimics GR quite well.

We mention in passing that (1.2) can be ‘linearized’ by introducing the dimensionless field ψ :=√φ/c, in terms of which (1.2) reads:

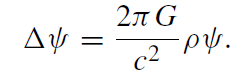 (1.3)

The boundary conditions are now ψ(r → ∞) → 1. Hence only those linear combinations of solutions whose coefficients add up to one are again solutions. For  ρ ≥ 0 it also follows that solutions to (1.3) can never assume negative values, since otherwise the function ψ must have a negative minimum (because of the positive boundary values) and therefore non-negative second derivatives are there. But then (1.3) cannot be satisfied at the minimum, hence ψ must be non-negative everywhere. This implies that solutions of (1.2) are also non-negative. To be sure, for mathematical purposes (1.3) is easier to use than (1.2), but note that φ and not ψ is the physical gravitational potential.

We now show how these nonlinear features render impossible the notion of a point mass, and even induce a certain black hole behaviour on their solutions. Let us be interested in static, spherically symmetric solutions to (1.2) with source ρ, which is zero for r > R and constant for r < R. We need to distinguish two notions of mass. One mass just counts the amount of ‘stuff’ located within r < R. You may call it the ‘bare mass’ or ‘baryonic mass’, since for ordinary matter it is proportional to the baryon number. We denote it by MB. It is simply given by

. (1.4)

The other mass is the ‘gravitational mass’, which is measured by the amount of flux of the gravitational field to ‘infinity’, that is, through the surface of a sphere whose radius tends to infinity. We call this mass M_G. It is given by

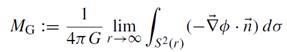 (1.5)

where 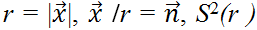is the two-sphere of radius r and dσ is its surface element. M_G should be identified with the total inertial mass of the system, in full analogy to the ADM mass in GR. Hence M_Gc² is the total energy of the system, with gravitational binding energy also taken into account. The masses M_B and M_G can dimensionally be turned into radii by writing R_B := GM_B/c² and R_G := GM_G/c², and further turned into dimensionless quantities via rescaling with R, the radius of our homogeneous star. We write x := R_B/R and y := R_G/R.

For each pair of values for the two parameters M_B and R there is a unique homogeneous-star solution to (1.2), whose simple analytical form need not interest us here. Using it we can calculate M_G, whose dependence on the parameters is best expressed in terms of the dimensionless quantities x and

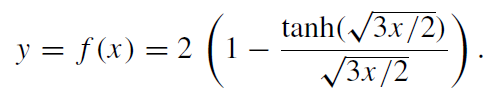 (1.6)

The function f maps the interval [0,∞] monotonically to [0, 2]. This implies the following inequality

M_G < 2Rc²/G    (1.7)

which says that the gravitational mass of the star is bounded by a purely geometric quantity. It corresponds to the statement in GR that the star's radius must be bigger than its Schwarzschild radius, which in isotropic coordinates is indeed given by R_S = GM_G/2c². It can be proven that the bound (6.7) still exists for non-homogeneous spherically symmetric stars, so that the somewhat unphysical homogeneity assumption can be lifted. The physical reason for this inequality is the ‘redshift’, i.e. the fact that the same bare mass at lower gravitational potential produces less gravitational mass. Hence adding more and more bare mass into the same volume pushes the potential closer and closer to zero (recall that φ is always positive) so that the added mass becomes less and less effective in generating gravitational fields. The inequality then expresses the mathematical fact that this ‘redshifting’ is sufficiently effective so as to give finite upper bounds to the gravitational mass, even for unbounded amounts of bare mass.

The energy balance can also be nicely exhibited. Integrating the matter energy density φρ and the energy density of the gravitational field, c⁴/8πG (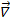φ/ )², we obtain

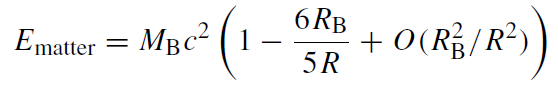 (1.8)

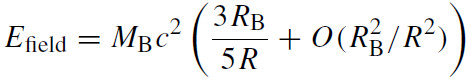 (1.9)

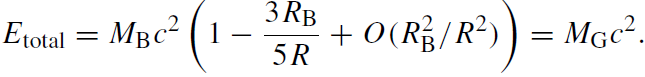 (1.10)

Note that the term −3M_Bc²R_B/5R in (1.10) is just the Newtonian binding energy. At this point it is instructive to verify the remarks we made earlier about the positivity of the gravitational energy. Shrinking a mass distribution enhances the field energy, but diminishes the matter energy twice as fast, so that the overall energy is also diminished, as it must be due to the attractivity of gravity. But here this is achieved with all involved energies being positive, unlike in Newtonian gravity. Note that the total energy, M_G, cannot become negative (since φ cannot become negative, as has already been shown). Hence one also cannot extract an infinite amount of energy by unlimited compression, as is possible in Newtonian gravity. This is the analogue in our model theory to the positive mass theorem in GR.

We conclude by making the point announced earlier, namely that the inequality (1.7) shows that point objects of finite gravitational mass do not exist in the theory based upon (1.2); mass implies extension! Taken together with the lesson from special relativity, that extended rigid bodies also do not exist (since the speed of elastic waves is less than c), we arrive at the conclusion that the dynamical problem of gravitating bodies and their interaction is fundamentally field theoretic (rather than point mechanical) in nature. Its proper realization is GR to which we now turn.