


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 12-2-2017
Date: 23-12-2015
Date: 2-2-2017
|
The relation between black holes and bulges
Black hole mass and bulge mass/luminosity
In recent years, there has been mounting evidence that black holes may be a normal, possibly ubiquitous, component of galaxies: if a galaxy has a bulge or is an elliptical, we expect to find a massive black hole in its center.
The masses of the suspected black holes have been obtained (or estimated) by a variety of methods, some more reliable than others. The mass determination for the Galactic black hole is, of course, outstanding in its accuracy and resolution, and is discussed in detail elsewhere. Very reliable black hole masses can also be obtained by very high resolution radio-interferometric observations of maser disks around central massive objects. Unfortunately, this method can be applied to only a very few objects, since a special disk geometry is required. In the best case, the Keplerian disk rotation under the influence of the central point source can be measured directly, making the estimate for the black hole mass, M•, very secure. This has, however, only been achieved in one case, NGC 4258 (Miyoshi et al 1995, Herrnstein et al 1999, Bragg et al 2000).
The determination of the velocity structure of a central dust disk yields another reliable mass estimate. Of course, the galaxy under investigation must have such a very central dust disk that can be studied without too much extinction. This restricts the usefulness of the method to a few elliptical galaxies with central disks of dust and ionized gas that can be resolved (at least by the HST, the Hubble Space Telescope). The black hole masses determined forM84 (Bower et al 1998) and NGC 7052 (van der Marel and van den Bosch 1998) are good examples of a successful application of this method.
Most black hole masses have been estimated by means of stellar dynamics, from either HST or ground-based data. Here, the goal is to measure the rise of the velocity dispersion due to the influence of the central mass. In principle, this method can be and has been applied to many galaxies, and the first study of black hole demographics was based on values for M• determined by stellar dynamics (Magorrian et al 1998). However, sufficient resolution is an issue here the ‘sphere of influence’ of the black hole has to be clearly resolved. This is a difficult task: in a number of cases the rise of the velocity dispersion assigned to the black hole was only observed in the central pixel.
A relatively new and very promising technique for determining M● is reverberation mapping of Active Galactic Nuclei (AGNs). In this method, time delays between brightness variations in the continuum and in the broad line emission region (BLR) are interpreted as the light travel time between the black hole and the BLR, i.e. the black hole accretion disk. Velocity information comes from the width of the emission lines, and thus the black hole mass can be determined as M● ≈ V2r/G. The obvious advantage of this method is that it is independent of distance. Thus, obtaining M● for a large number of AGNs, mostly too far away for the more classical techniques, becomes possible (see Gebhardt et al 2000a, Kaspi et al 2000, Wandel et al 1999). It now seems that this method yields results that are very consistent with reliable determinations by other means.
In any case, in recent years, enough black hole masses have been determined for it to become worthwhile to look for relations between M● and host galaxy parameters, especially those of the oldest component of a galaxy, the bulge.
The beginnings of what is now known as the relation between bulge and M● were rather humble and go back to at least Kormendy (1993). There seemed to be evidence that M● scales with the luminosity (equivalent to the mass for a constant M/L ratio) of the bulge. In a 1995 review paper, Kormendy and Richstone displayed a diagram relating the mass of the bulge to M● for eight galaxies (and two non-detections). Excluding the mass determination for the Galactic black hole, which seemed to have a mass that was too low in relation to the other estimates, they found a proportionality of M●/Mbulge ∼ 3 × 10−3. The Galactic black hole alone yielded M●,gal/Mbulge,gal ∼ 1.7×10−4. Even then, the question could be asked why the best-determined value (for the Galaxy) was excluded from the relation. But at that time, the relation was based on very few galaxies and had to be considered more as a trend than a firm proportionality.
In their paper on the demography of black holes in galaxy centers, Magorrian et al (1998) investigated the stellar kinematics of 32 galaxies. After careful modelling of the bulge kinematics to obtain M●, they found a relation between M● and Mbulge of the form

From individual galaxy data, a proportionality of {M●/Mbulge} ∼ 0.016 can be derived if the unrealistically high value found for NGC 4486B is included. If this galaxy is excluded, the ratio drops to 7 × 10−3.
Following these results that seemed to indicate that a relation between black hole and bulge mass really existed, albeit with a substantial scatter, a potential problem was pointed out by a number of authors (e.g. Wandel 1999, Ho 1999). The new masses determined by reverberation mapping seemed to be systematically low compared to the stellar dynamical masses. In addition, the large ratio suggested was not compatible with the black hole mass density inferred if the optical QSO luminosity was to be reproduced by (standard) accretion onto black holes.
Black hole mass and bulge velocity dispersion
A revision of the M●-Mbulge relation and a possible breakthrough became public in two letters published back to back in the same issue of Astrophysics. J. Ferrarese and Merritt (2000) and Gebhardt et al (2000b) independently presented a new, much tighter relation between M● and the bulge velocity dispersion σ (see figure 1.1).
Ferrarese and Merritt first sorted black hole masses from the literature into groups of ‘reliable’ and ‘unreliable’ values, with many of the (especially ground based) masses from the Magorrian et al sample in the latter category, since Ferrarese and Merritt suspected that in many cases the black hole's sphere of influence was unresolved. However, the scatter in the M●-Mbulge relation did not decrease when only the better determined masses were considered. This changed dramatically when σ instead of the bulge mass was correlated with M●. While the scatter was still large for the galaxies with the uncertain black hole masses, the relation for the 12 galaxies with ‘good’ values for M● became very tight. Gebhardt et al (a large group of scientists overlapping strongly with the authors of the Magorrian et al work) found exactly the same effect for a different sample of galaxies and values for M● based on stellar dynamics, mostly done with very high resolution data obtained from the HST.
The relationship is so tight that it is statistically ‘perfect’ in the sense of being compatible with only having errors due to measurements, i.e. no intrinsic scatter. This is almost ‘embarrassingly’ tight (Merritt and Ferrarese 2001c), since a relation this close has to be explained with effects of galaxy assembly and evolution. If confirmed, this relation may be used to predict black hole masses accurately from the much more easily obtained bulge velocity dispersion. The black hole masses found are significantly, by up to an order of magnitude, lower than the masses claimed before. Thus, the ratio between M● and Mbulge (which of course still has a larger scatter) has gone down to a value ∼ 2×10−3. This solves
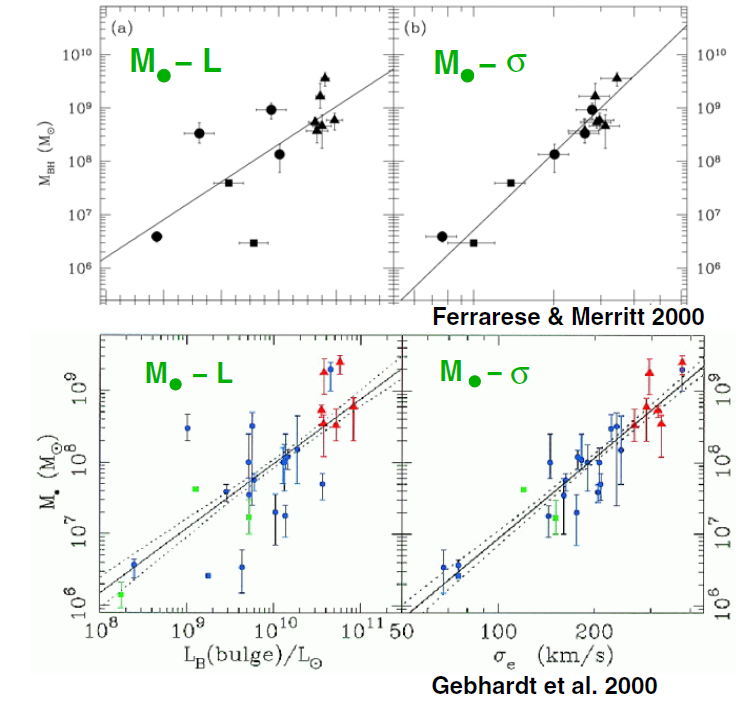
Figure 1.1. Upper panels: the M●-σ relation according to Ferrarese and Merritt (2000). The left panel shows the large scatter in the M●-Lbulge relation. For the same sample of galaxies, the scatter is greatly reduced if M● is related to σ instead. Lower panels: Gebhardt et al (2000b) come to the same conclusion, using a different sample of galaxies.
a number of problems: first, the extremely well-determined mass of the Galactic black hole is now almost consistent with the general relation. Second, and maybe more fundamentally important, the density of black holes in the local universe has been redetermined to be ρ● ≈ 5 × 105Mּ Mpc−3. This is to be compared to the prediction of the QSO luminosity function: ρ● ≈ (2–3) × 105Mּ Mpc−3. Thus, very little, if any, ‘invisible’ black hole growth since the quasar epoch is required.
Despite the general agreement, some problems remain. The relations found by the two groups differ in detail: Merritt and Ferrarese find
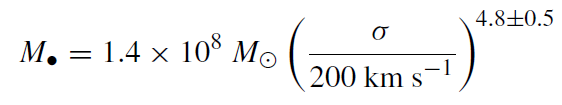
while Gebhardt et al obtain
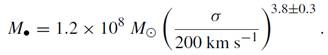
The different slope may be partly due to a different sample. However, if the relation really has no (or extremely low) intrinsic scatter, it should of course be identical no matter what sample is chosen. There are also differences in the statistical analysis of the data (Merritt and Ferrerese 2001a, b), which contribute to the discrepancy.
It is, at this time, difficult to say whether these differences (in data, method and opinion) only concern details which will be easily sorted out when more and better data become available or whether they touch on fundamental difficulties. Part of the current discussion concerns a possible low-mass cut-off of the relation, with the test case of the Local Group galaxy M 33, a galaxy that has (almost?) no bulge and is sufficiently nearby to allow very sensitive searches for the signature of a black hole. No black hole has been found so far down to the very low mass limit of M● < 3000 Mּ (Merritt et al 2001). Obviously, the implications of such a mass cut-off for the M●-σ relation are related to its slope.
In any case, the impact of the M●-σ relation on studies of galaxy formation and early evolution will very likely be significant. Clearly, it ‘must be telling us something fundamental about origins (galaxy formation) and the connection between black hole mass and bulge properties’ (Merritt and Ferrarese 2001a). If the relation is simply interpreted as the M●-Mbulge relation recast in another form, it implies the well-known Faber-Jackson law for elliptical galaxies (which relates the velocity of stars to the bulge luminosity), and thus corresponds to a (not entirely explained) fundamental plane relation, even with approximately the right slope (Mbulge ∼ σ5).
However, as we have seen, the M●-σ relation appears much tighter. As a constraint, it has to survive subsequent mergers in the scenario of hierarchical structure formation without being disrupted. Fundamental plane relations also survive merging, but are generally less tight. To add to the ‘problem’, it appears that another very close relation may have been found very recently: Graham et al (2001) report that the correlation between M● and the light concentration within a bulge's half-light radius is as tight (in fact, statistically slightly tighter) as the M●-σ relation. Since the central condensation can be determined from surface photometry alone, it might be possibly to estimate M● from fairly simple observations. In any case, it is probably necessary to look for an additional feedback mechanism during bulge formation that directly connects the black hole mass, the stellar velocity dispersion and possibly (if the Graham et al result is confirmed) the central light concentration.
Some possibilities for explaining the M●-σ relation have been suggested, one even before its discovery (Silk and Rees 1998). They propose that black holes form even before bulges from the collapse of ∼ 106Mּ gas clouds, which then accrete and radiate. This drives a wind which acts back on the accretion flow. In this scenario, the black holes have to form very early. Alternatively, black holes can be thought to grow naturally in mergers. The feedback may then be supplied by gas cooling balanced by energy input through supernovae. The impact of this energy input may be stronger for smaller galaxies with shallower gravitational potentials (Kauffmann and Haehnelt 2000, Haehnelt and Kauffmann 2000). Burkert and Silk (2001) also consider black hole growths in mergers, but suggest a somewhat different feedback mechanism: in their model, the accretion is halted when star formation begins to exhaust the gas supply in the outer accretion disk.
All these models result in an M●-σ relation with roughly the expected slope, at least after some fine-tuning. However, they all have problems in explaining why the relation appears so tight. Thus, much work, both observationally and theoretically, remains to be done until the role of the M●-σ relation in the process of galaxy evolution is fully understood.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|