
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Scalar massless field in the Schwarzschild metric
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 149
2-2-2017
1958
Scalar massless field in the Schwarzschild metric
1.1 Field equation
The electromagnetic field and gravitational perturbations are of most interest in astrophysical applications. Both fields are massless and carry spin. For simplicity, we consider first a massless scalar field with zero spin and discuss later effects caused by spin. Moreover, we consider the simpler case of a non-rotating black hole.
A massless scalar field evolves according to the Klein-Gordon equation
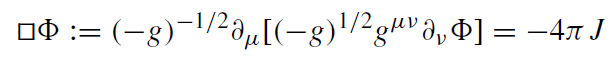 (1.1)
(1.1)
where g is the determinant of the metric gμν and J a scalar charge density.
1.2 Spherical reduction
In a general spherically symmetric spacetime with metric
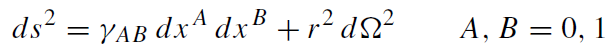 (1.2)
(1.2)
one can decompose a general solution into the spherical modes
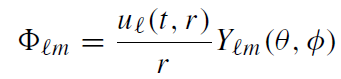 (1.3)
(1.3)
where Yℓm(θ, φ) are the spherical harmonics. The functions uℓm obey the two dimensional wave equation
 (1.4)
(1.4)
where 2□ = (−γ)−1/2∂A[(−γ)1/2γ AB∂B] is the two-dimensional ‘box’ operator for the metric γAB, and
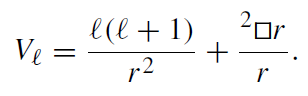 (1.5)
(1.5)
For the Schwarzschild metric, we find
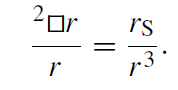 (1.6)
(1.6)
1.3 Radial equation and effective potential
We focus now on solutions of the homogeneous equations with jℓm = 0. Since the Schwarzschild geometry is static we can decompose them into monochromatic waves
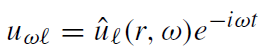 (1.7)
(1.7)
where the radial function ûℓ(r, ω) is a solution of the equation
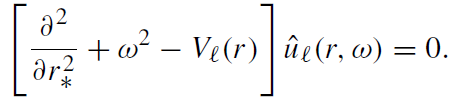 (1.8)
(1.8)
Here r∗ is the so called tortoise coordinate
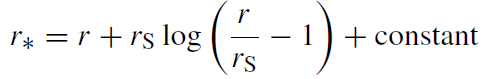 (1.9)
(1.9)
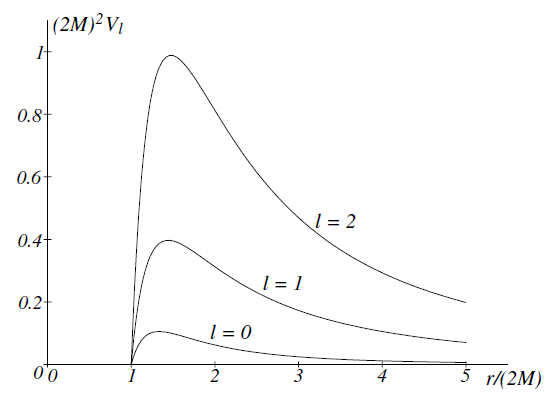
Figure 1.1. The effective potential Vℓ for ℓ = 0, 1, 2 as a function of r .
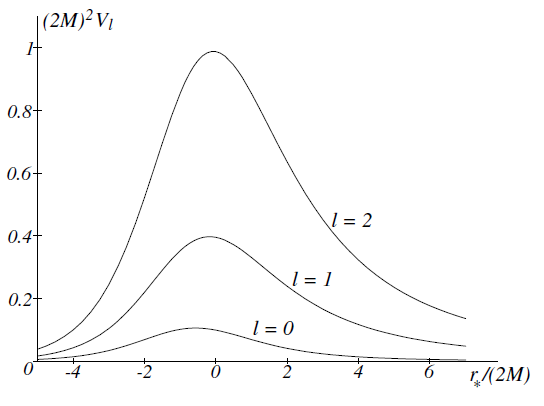
Figure 1.2. The same potentials as functions of r∗. The constant in the definition of r∗ is fixed so that r∗ = 0 for r = 3M.
and Vℓ(r ) is the effective potential
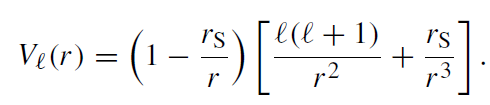 (1.10)
(1.10)
The effective potential for different values of ℓ is shown in figures 1.1 and 1.2. The maximum of the effective potential Vℓ(r ) is roughly at the location of the unstable circular photon orbit (r = 3M).
The form of the radial wave equation is similar to the quantum mechanical equation for one-dimensional potential scattering and hence most problems concerning perturbed black holes involve elements familiar from potential scattering in quantum mechanics. One would, for example, expect waves of short wavelength λ << rS to be easily transmitted through the barrier. Waves with λ ≈ rS will be partly transmitted and partly reflected, and finally waves with λ >> rS should be completely reflected by the black hole barrier.
1.4 Basic solutions
Let us consider two linearly independent solutions of the radial wave equations which have the following asymptotic forms
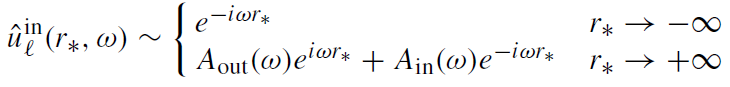 (1.11)
(1.11)
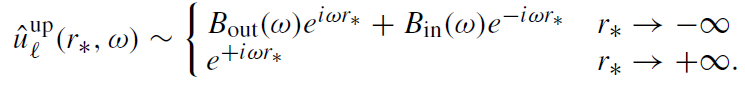 (1.12)
(1.12)
They are known as IN and UP modes, respectively. The complex conjugates of these solutions are also solutions of the radial wave equation. They are known as OUT and DOWN modes, respectively. For any two solutions u1 and u2 the Wronskian
 (1.13)
(1.13)
is constant. Calculating the Wronskian for solutions ûinℓ and ûupℓ and their complex conjugates and using their asymptotics, one obtains the following relations:
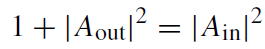 (1.14)
(1.14)
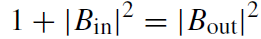 (1.15)
(1.15)
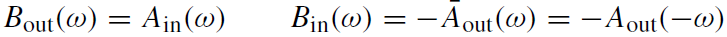 (1.16)
(1.16)
and
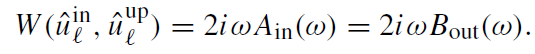 (1.17)
(1.17)
Since |Ain| ≥ 1, the solutions ûinℓ and ûupℓ are linearly independent.
1.5 Interpretation of basic solutions
Let us discuss the physical meaning of the basic solutions. By combining the radial solutions with exp(-iωt) we get functions describing wave propagation. They have simple physical interpretations. The DOWN solution satisfies the boundary condition that there is no radiation escaping to infinity. This means that exactly the right amount of radiation with just the right phase must emerge from the past horizon H− in order to cancel any radiation that might otherwise be scattered back to infinity from a wave originally incoming from past infinity.
Thus, in this solution, there is radiation coming in from infinity, radiation emerging from H− to meet it, and radiation going down the black hole at H+. The amplitudes of the various waves are such that down is an acceptable solution to the radial wave equation. The UP mode is defined analogously by the boundary condition that there be no incoming radiation from infinity. In a similar way the IN solution does not contain radiation outgoing from H−, while the OUT mode has no radiation going down the black hole at H+. The situation is presented graphically in figure 1.3.
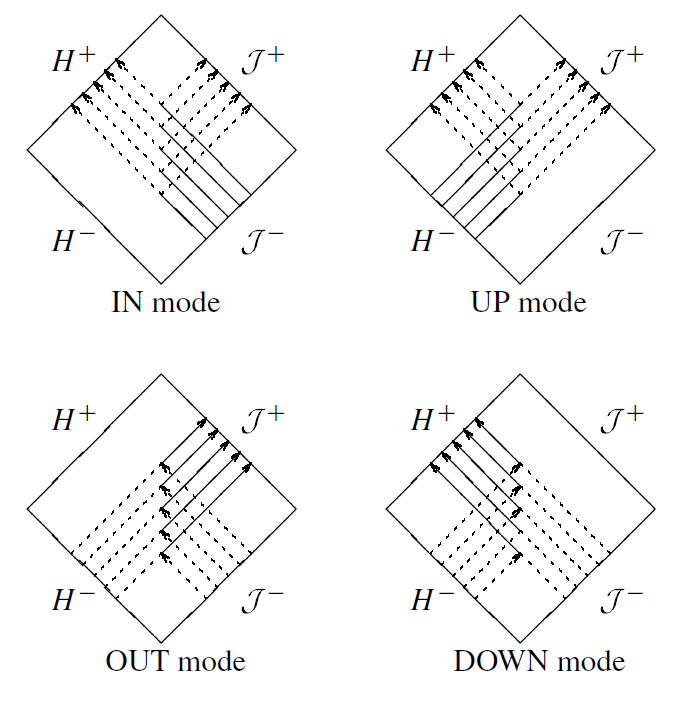
Figure 1.3. IN, UP, OUT and DOWN modes.
One can use the diagrams presented in figure 1.3 as mnemonic rules for the definition of the basic functions. The regions inside the squares represent the spacetime in the exterior of the eternal version of the black hole. The straight lines at the angle of π/4 represent null rays. Two boundaries  + and
+ and  − correspond to asymptotic future and past infinities. The other two boundaries H+ and H− are the event horizon and the past horizon, respectively. This type of diagram can be obtained by special conformal transformations that bring infinitely distant points of the spacetime to a finite distance. The corresponding Penrose-Carter conformal diagram proved to be a very powerful tool for the study of the global structure of spacetime. Asymptotic values of massless fields in an asymptotically flat physical spacetime are related to the boundary values at the null surfaces
− correspond to asymptotic future and past infinities. The other two boundaries H+ and H− are the event horizon and the past horizon, respectively. This type of diagram can be obtained by special conformal transformations that bring infinitely distant points of the spacetime to a finite distance. The corresponding Penrose-Carter conformal diagram proved to be a very powerful tool for the study of the global structure of spacetime. Asymptotic values of massless fields in an asymptotically flat physical spacetime are related to the boundary values at the null surfaces 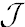 + and
+ and 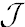 −, representing the so-called future and past null infinities.
−, representing the so-called future and past null infinities.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















