


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Elementary Theory of integration -The Darboux Integral for Functions on RN |
|
|
|
Read More
Date: 1-12-2016
Date: 23-11-2016
Date: 30-11-2016
|
Elementary Theory of integration -The Darboux Integral for Functions on RN
The reader is undoubtedly familiar with the idea of the integral and with methods of performing integrations. In this section we define the integral precisely and prove the basic theorems for the processes of integration.
Let f be a bounded function whose domain is a closed interval I ={x : a ≤ x ≤ b}. We subdivide I by introducing points t1,t2,...,tn−1 that are interior to I. Setting a = t0 and b =tn and ordering the points so that t0 < t1 <t2 <...<tn, we denote by I1,I2,...,In the intervals Ii ={x : ti−1 ≤ x ≤ ti}. Two successive intervals have exactly one point in common. (See Figure 1.1.) We call such a decomposition of I into subintervals a subdivision of I, and we use the symbol Δ to indicate such a subdivision. Since f is bounded on I, it has a least upper bound (l.u.b.), denoted by M. The greatest lower bound (g.l.b.) of f on I is denoted by m. Similarly, Mi and mi denote the l.u.b. and g.l.b., respectively, of f on Ii . The length of the interval Ii is ti − ti−1; it is denoted by l(Ii).
Definitions
The upper Darboux sum of f with respect to the subdivision Δ , denoted S+(f,Δ), is defined by(1.1)
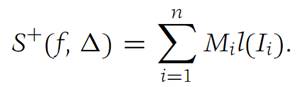
Similarly , the lower Darboux sum, denoted S−(f,Δ), is defined by(1.2)
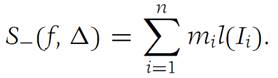

Figure 1.1 A subdivision of I.
Suppose Δ is a subdivision a =t0 <t1 < ... < t n−1 <tn = b, with the corresponding intervals denoted by I1,I2,...,In. We obtain a new subdivision by introducing additional subdivision points between the various {ti}. This new subdivision will have subintervals I/1,I/2,...,I/m each of which is a part (or all) of one of the sub intervals of Δ. We denote this new subdivision by Δ/and call it a refinement of .
Suppose that Δ1 with subintervals I1,I2,...,In and that Δ2 with subintervals J1,J2,...,Jm are two subdivisions of an interval I. Wegetanew subdivision of I by taking all then dpoints of the subintervals of bothΔ1 and Δ2, arranging them in order of increasing size, and then labeling each subinterval having as its endpoints two successive subdivision points. Such a subdivision is called the common refinement ofΔ1 and Δ2, and each subinterval of this new subdivision is of the form Ii ∩ Jk, i = 1, 2,...,n, k = 1, 2,...,m. Each Ii ∩ Jk is either empty or entirely contained in a unique subinterval (Ii) of Δi and a unique subinterval (Jk) of Δ2. An illustration of such a common refinement is exhibited in Figure
1.2.
Theorem 1.1
Suppose that f is a bounded function with domain I ={x:a ≤ x ≤ b}. Let Δ be a subdivision of I and suppose that M and m are the least upper bound and greatest lower bound of f on I, respectively. Then
(a)m(b − a) ≤ S−(f,Δ) ≤ S+(f,Δ) ≤ M(b − a).
(b) If Δ/is a refinement of Δ, then S−(f,Δ) ≤ S−(f,Δ/) ≤ S+(f,Δ/) ≤ S+(f, Δ).
(c) If Δ1 and Δ2 are any two subdivisions of I, thenS−(f,Δ1) ≤ S+(f,Δ2).
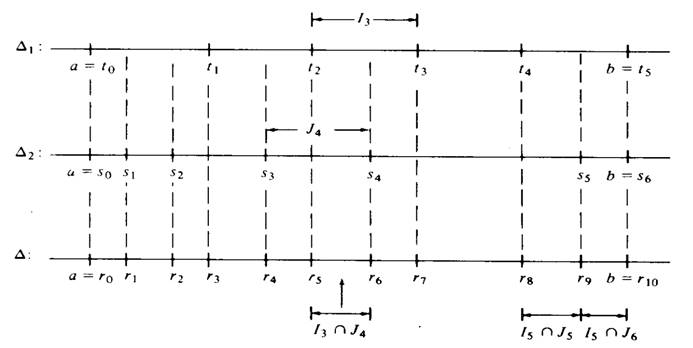
Figure 1.2 A common refinement.
Proof
(a) From the definition of least upper bound and greatest lower bound, we have
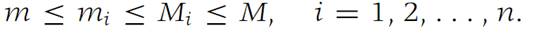
Also
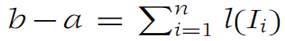
Thus the inequalities in part (a) are an immediate consequence of the definition of S+ and S− as given in equations (1.1) and(1.2):
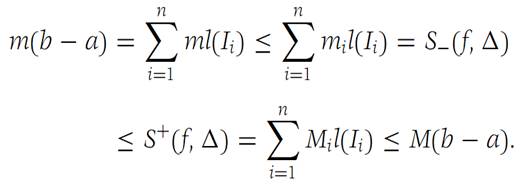
(b) To prove part (b), let Δi be the subdivision of Ii that consists of all those intervals of Δ/ that lie in Ii . Since each interval of Δ/ is in a unique Δi we have, applying part (a) to each Δi ,
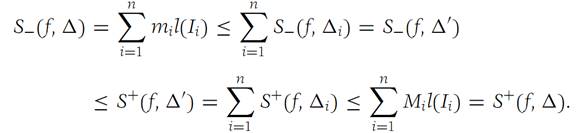
(c) To prove part (c), let Δ be the common refinement of Δ1 and Δ2. Then, using the result in part (b), we obtain
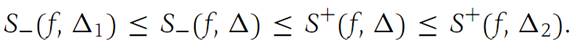
Definitions
If f is a function on R1 that is defined and bounded on I ={x : a ≤ x ≤ b}, we define its upper and lower Darboux integrals by
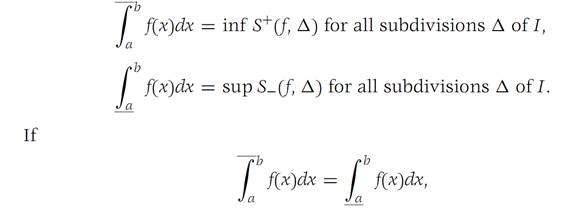
we say that f is Darboux integrable, or just integrable, on , and we designate the common value by
The following results are all direct consequences of the above definitions.
Theorem 1.2
If m ≤ f(x) ≤ M for all x ∈ I ={x: a ≤ x ≤ b}, then
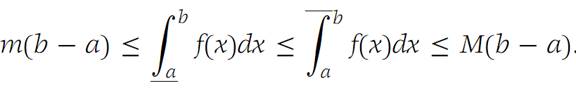
Proof
LetΔ1 andΔ2 be subdivisions of I. Then from parts (a) and (c) of Theorem 1.1, it follows that

We keep Δ1 fixed and let Δ2 vary over all possible subdivisions. Thus S+(f,Δ2) is alwayslarger than or equal to S−(f,Δ1), and so its greatest lower bound is alwayslarger than or equal to S−(f,Δ1). We conclude that
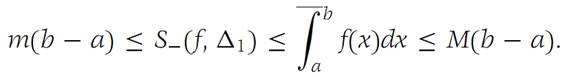
Now letting Δ1 vary over all possible subdivisions, we see that the least upper bound of S−(f,Δ1) cannot exceed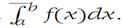 The conclusion of the theorem follows.
The conclusion of the theorem follows.
The next theorem states simple facts about upper and lower Darboux integrals. The results all follow from the definitionsof inf, sup, and upper Darboux and lower Darboux integrals.
Theorem 1.3
Assuming that all functions below are bounded, we have the following formulas:(a) If g(x) = kf (x) for all x ∈ I ={x: a ≤ x ≤ b} and k is a positive number,
Then

Corollary
If the functions considered in Theorem 1.3 are Darboux integrable, the following formulas hold:

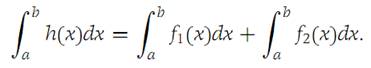
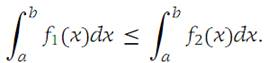
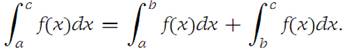
It is useful to define
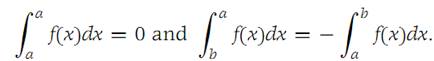
Then formula (1.3) above is valid whether or not b is between a and c so long as all the integrals exist. It is important to be able to decide when a particular function is inte grable. The next theorem gives a necessary and sufficient condition for integrability.
Theorem 1.4
Suppose that f is bounded on an interval I ={x: a ≤ x ≤ b}. Then f is integrable ⇔ for every Ԑ> 0 there is a subdivision Δ of I such that
S+(f,Δ) − S−(f,Δ) <Ԑ.
Suppose that condition (1.4) holds. Then from the definitions of upper and lower Darboux integrals, we have
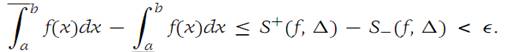
Since this inequality holds for every Ԑ> 0 and the left side of the inequality is independent of Ԑ, it follows that
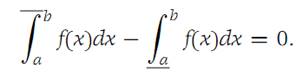
Hence f is integrable.
Now assume that f is integrable; we wish to establish inequality (1.4).
For any Ԑ> 0 there are subdivisions Δ1 and Δ2 such that(1.5)
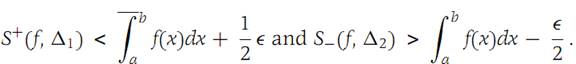
We choose Δ as the common refinement of Δ1 and Δ2. Then (from Theorem 1.1)
Substituting inequalities (1.5) into the above expression and using the fact that

As required.
If f is continuous on the closed interval I ={x: a ≤ x ≤ b}, then f is integrable.
The function f is uniformly continuous, and hence for any Ԑ> 0 there Is a δ such that

Choose a subdivision Δ of I such that no subinterval of Δ has length larger than δ. This allowsus to establish formula (1.4), and the result follows from Theorem 1.4.
Theorem 1.5(Mean-value theorem for integrals).
Suppose that f is continuous on I ={x: a ≤ x ≤ b}. Then there is a number ξ in I such that
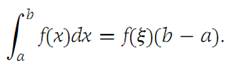
According to Theorem 1.2, we have(1.6)
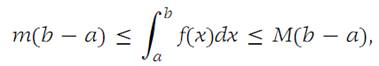
where m and M are the minimum and maximum of f on I, respectively. From the Extreme-value theorem there are numbers x0 and x1 ∈ I such that f(x0)= m and f(x1) =M. From inequalities (1.6) it follows that
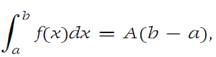
where A is a number such that f(x0) ≤ A ≤ f(x1). Then the intermediate value theorem show that there is a number ξ ∈ I such that f(ξ)= A.
We now present two forms of the Fundamental theorem of calculus, a result that shows that differentiation and integration are inverse processes.
Theorem 1.6(Fundamental theorem of calculus—first form).
Suppose that f is continuous on I ={x:a ≤ x ≤ b}, and that F is defined by
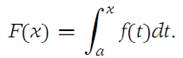
Then F is continuous on I, and F/(x) =f(x) for each x ∈ I1 ={x: a<x<b}.
Since f is integrable on every subinterval of I, we have
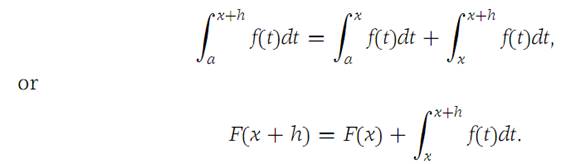
We apply the Mean-value theorem for integrals(Theorem 1.5) to the last term on the right, getting
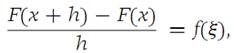
where ξ is some number between x and x + h. Now, let 8> 0 be given.
There is a δ> 0 such that |f(y) − f(x)| <Ԑ for all y on I1 (taking ξ y) with |y − x| <δ. Thus, if 0 < |h| <δ, we find that
Theorem 1.7(Fundamental theorem of calculus—second form).
Suppose that f and F are continuous on I ={x:a ≤ x ≤ b} and that F/(x) = f(x) for each
x ∈ I1 ={x:a<x<b}. Then(1.7)
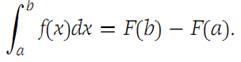
We consider a subdivision Δ of I. We write

We apply the Mean-Value theorem to each term in the sum. Then as the
mesh size tends to zero we get (1.7).
1. Compute S+(f,Δ) and S−(f,Δ) for the function f : x → x2 defined on I ={x :0 ≤ x ≤ 1} where Δ is the subdivision of I into 5subintervals of equal size.
2. (a) Given the function f : x → x3 defined on I ={x :0 ≤ x ≤ 1},suppose Δ is a subdivision and Δ/is a refinement of Δ that adds one more point. Show that S+(f,Δ/)<S+(f,Δ) and S−(f,Δ/)>S−(f, Δ).
(b) Give an example of a function f defined on I such that S+(f,Δ/ ) = S+(f,Δ) and S−(f,Δ/) =S−(f,Δ)
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(81-89)



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|