


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Basic Properties of Functions on R1 -The Bolzano–Weierstrass Theorem |
|
|
|
Read More
Date: 23-11-2016
Date: 1-12-2016
Date: 22-11-2016
|
Suppose that
(1.4) x1,x2,...,xn,...
is a sequence of numbers. Then the sequences x1,x3,x5,... and x2,x5,x8,x11,... are examples of subsequences of (1.4). More generally, suppose that k1,k2,k3,...,kn,... is an increasing sequence of positive integers. Then we say that
xk1 ,xk2 ,...,xkn ,...
is a subsequence of (1.4). The choice k1 = 1,k2 = 3,k3 = 5,k4 = 7,... is an example of a subsequence of (1.4) above. To avoid double subscripts, which are cumbersome, we will frequently write y1 = xk1 ,y2 =xk2 ,...,yn = xkn ,..., in which case
y1,y2,...,yn,...
is a subsequence of (1.4).
We easily prove by induction that if k1,k2,k3,...,kn,... is an increasing sequence of positive integers, then kn ≥ n for all n .The sequence(1.5)
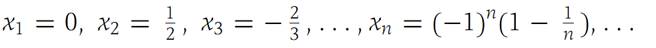
has the subsequences
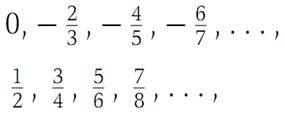
which are obtained from (1.5) by taking the odd-numbered terms and the even-numbered terms, respectively. Each of these subsequences is convergent, but the original sequence (1.5) is not. The notion of a convergent subsequence of a given sequence occurs frequently in problems in analysis. The Bolzano–Weierstrass theorem is basic in that it establishes the existence of such convergent subsequences under very simple hypotheses on the given sequence.
Theorem 1.1 (Bolzano–Weierstrass Theorem)
Any bounded infinite sequence of real numbers contains a convergent subsequence.
Proof
We shall use the Nested intervals theorem (Theorem 3.1). Let {xn} be a given bounded sequence. Then it is contained in some closed interval I ={x : a ≤ x ≤ b}. Divide I into two equal subintervals by the midpoint (a + b)/2. Then either the left subinterval contains an infinite number of the {xn} or the right subinterval does (or both). Denote by I1 ={x : a1 ≤ x ≤ b1} the closed subinterval of I that contains infinitely many {xn}. (If both subintervals do, choose either one.) Next, divide I1 into two equal parts by it smidpoint. Either the right subinterval or the left subinterval of I1 contains infinitely many {xn}. Denote by I2 the closed subinterval that does. Continue this process, obtaining the sequence

with the property that each In contains xp for infinitely many values of p. Since bn − an =(b − a)/2n → 0 as n →∞, we may apply the Nested intervals theorem to obtain a unique number x0 contained in every In.
We now construct a subsequence of {xp} converging to x0. Choose xk1 to be any member of {xp} in I1 and denote xk1 by y1. Next choose xk2 to be any member of {xp} such that xk2 is in I2 and such that k2 >k1.We can do this because I2 has infinitely many of the {xp}. Set xk2 =y2. Next, choose xk3 as any member of {xp} in I3 and such that k3 >k2. We can do this because I3 also has infinitely may of the {xp}. Set xk3 = y3.We continue, and by induction obtain the subsequence y1,y2,...,yn,....By the method of selection we have

Since an → x0, bn → x0,as n →∞, we can apply the Sandwiching theorem to conclude that yn → x0 as n →∞.
Problems
In Problems1 through 7 decide whether or not the given sequence converges to a limit. If it does not, find, in each case, at least one convergent subsequence. We suppose n = 1, 2, 3,...
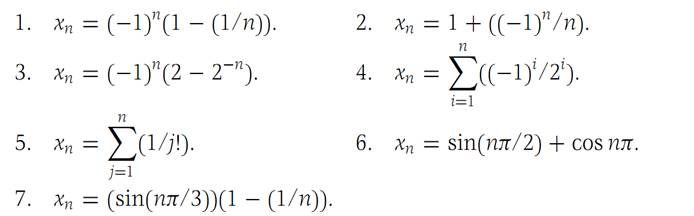
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(53 -55)



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|