


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 3-9-2016
Date: 11-8-2016
Date: 11-8-2016
|
Swing
A child of mass m on a swing raises her center of mass by a small distance b every time the swing passes the vertical position, and lowers her mass by the same amount at each extremal position. Assuming small oscillations, calculate the work done by the child per period of oscillation. Show that the energy of the swing grows exponentially according to dE/dt = αE and determine the constant α.
SOLUTION
Consider half a period of swinging motion between points 0 → 1 → 2 → 3 → 4 (see Figure 1.1, where the dotted line indicates the position of the center of mass). From 0 to 1, energy is conserved E0 = E1.
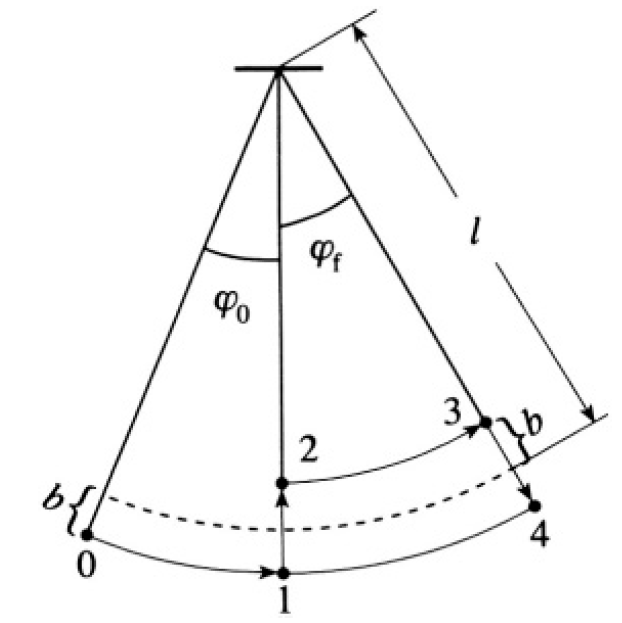
Figure 1.1
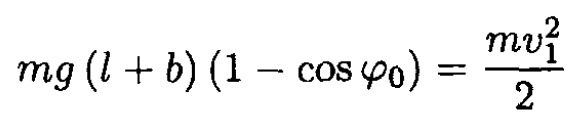
where φ0 is the initial angle. For small angles, 1- cos φ0 = φ20/2 and
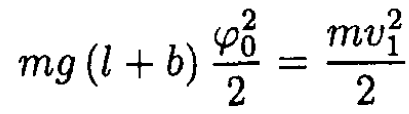 (1)
(1)
From 1 to 2, angular momentum is conserved:
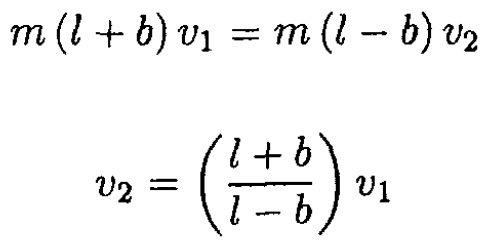 (2)
(2)
From 2 to 3, again, energy is conserved so we can find the final angle φf
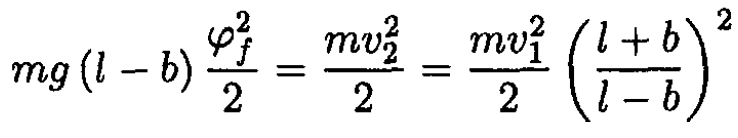 (3)
(3)
From (1) and (3) we can express mv21/2 and obtain the change in the amplitude:
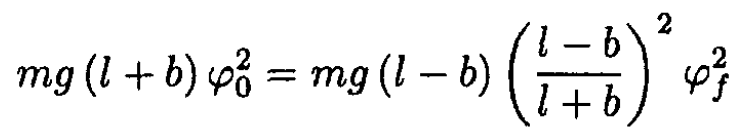 (4)
(4)
or using b/l << 1
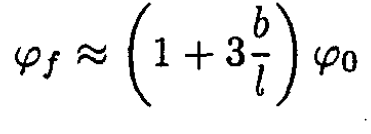 (5)
(5)
and
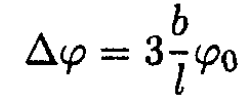 (6)
(6)
The work done by the child is equal to the energy change per period :
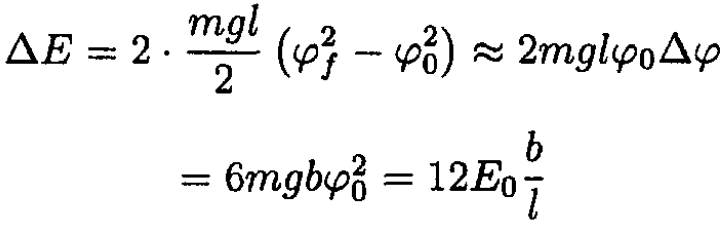 (7)
(7)
We want to write (7) in the form dE/dt = αE,
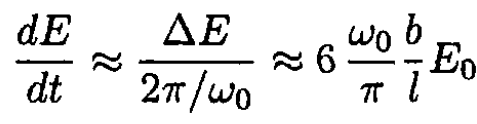 (8)
(8)
 (9)
(9)
where 



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|