


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 19-8-2016
Date: 10-9-2016
Date: 19-8-2016
|
Return of Heat Capacities
In a certain range of temperature τ and pressure p, the specific volume v of a substance is described by the equation
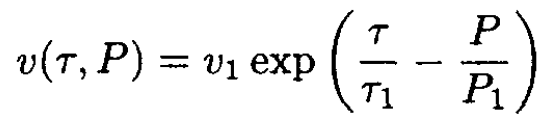
where v1, τ1, P1 are positive constants. From this information, determine (insofar as possible) as a function of temperature and pressure the following quantities:
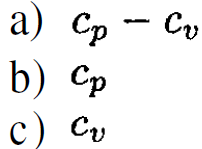
SOLUTION
a) We will again use the Jacobian transformation to find cp - cv as a function of τ, P.
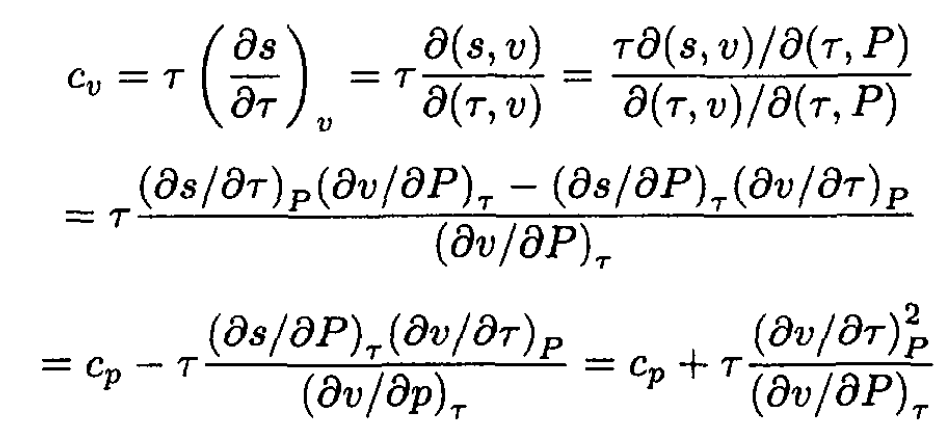 (1)
(1)
where we used
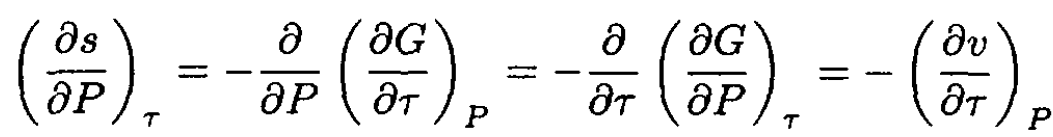
So, we obtain
 (2)
(2)
Substituting v(τ, P) into (2) yields
 (3)
(3)
b,c) We cannot determine the temperature dependence of cp or cv, but we can find cp (P) and cv (v), as follows:
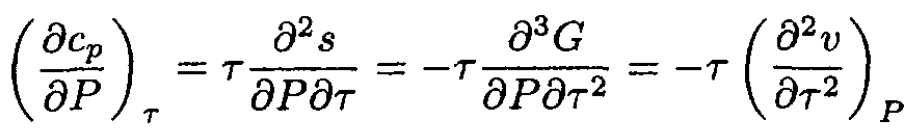 (4)
(4)
Similarly,
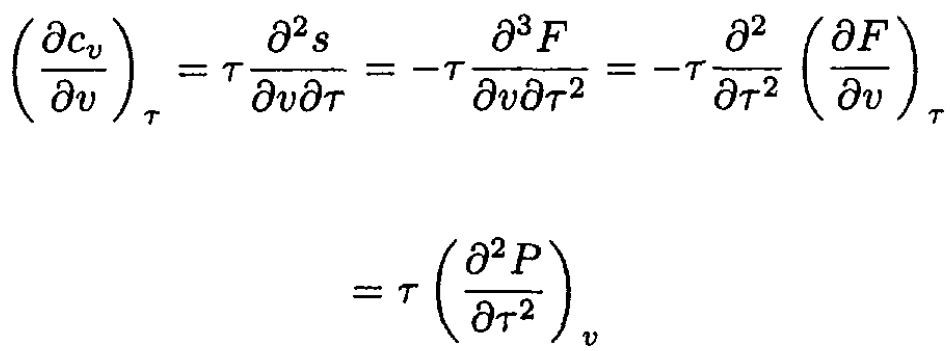 (5)
(5)
where F is the Helmholtz free energy, and we used
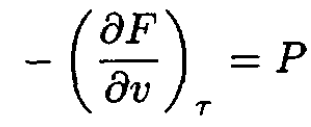
From (4) and the equation of state, we have
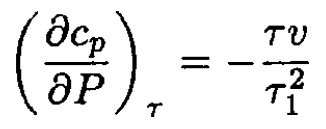 (6)
(6)
and from (5),
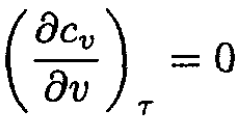 (7)
(7)
(since v = const implies τ/τ1 = P/P1). Integrating (6) and (7), we obtain
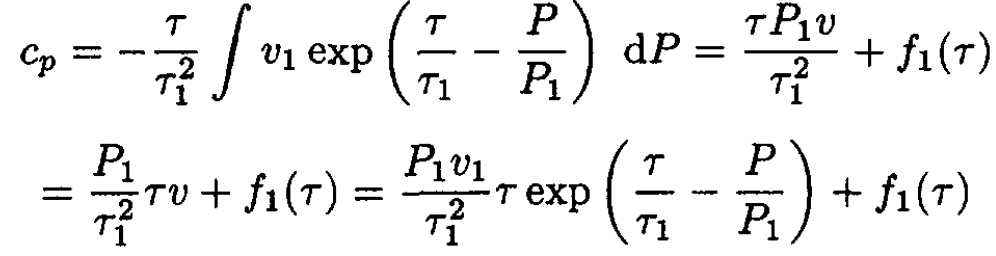 (8)
(8)
and
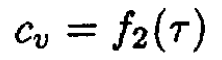 (9)
(9)
where f1 and f2 are some functions of temperature. Since we know cp - cv from (a), we infer that f1 = f2 ≡ f, and finally
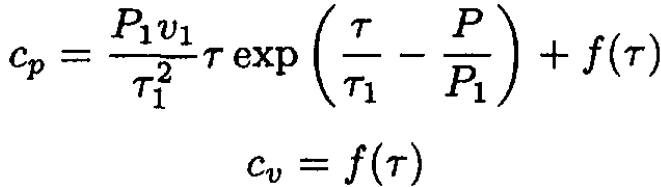 (10)
(10)



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|