Superconducting Sphere in Magnetic Field

A superconducting (Type I) spherical shell of radius R is placed in a uniform magnetic field B₀ (B₀ << H_c, H_c, the critical field). Find

a) the magnetic field everywhere outside the shell

b) the surface current density

Hint: Inside, B = 0.

SOLUTION

a) Prom symmetry considerations, it is clear that the current would flow on the surface of the shell perpendicular to the applied magnetic field. As for any ellipsoid in a uniform electric or magnetic field, we can assume that the field outside the shell produced by these currents is equivalent to a magnetic dipole moment m placed in the center of the shell. For

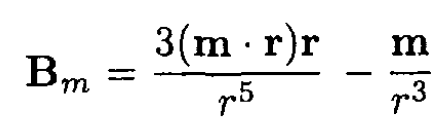
The total field outside is then B = B_m + B₀. The boundary condition on the surface at an arbitrary point gives

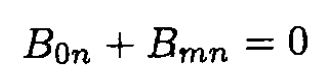
The normal component of B is continuous and inside B = 0. From the boundary conditions on the surface at an arbitrary angle θ between the direction of B₀ and the normal n (see Figure 1.1) we have

(1)

Figure 1.1

Hence

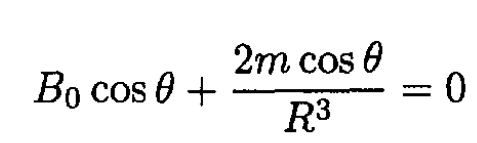(2)

At m = -(R³/2) B₀, where R is the radius of the spherical shell, the boundary conditions are satisfied on the surface of the shell. Therefore,

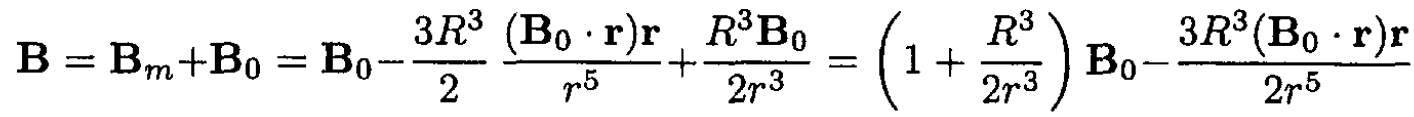
b) The surface current density J_s can be found by using tangential H component continuity:

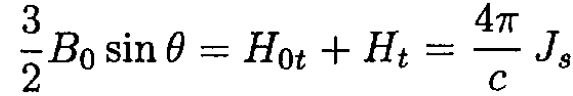
and therefore J_s(θ) = 3cB₀ sin θ/8π. This solution is only true while B < 2/3 H_c, and the whole sphere is superconducting. When B > 2/3 H_c the field at the equator exceeds H_c, and the sphere goes into an intermediate state.