


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 1-9-2019
التاريخ: 2023-02-11
التاريخ: 2024-02-24
التاريخ: 24-7-2016
|
قياس المجال الكهربائي في محاور اسناد مختلفة
بعد الملاحظات التجريبية التي اثبتت عدم تغير شحنة الجسيم المتحرك لابد من ايجاد علاقة تتعلق بالمجال الكهربائي لكي تبقى الشحنة ثابتة تحت تأثير تحويلات لورنس في جميع محاور الاسناد. فاذا قاس مشاهد في محور الاسناد s مجالا كهربائيا 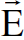 عند زمن معين، فما هو المجال الكهربائي الذي يقيسه المشاهد في محور الاسناد sʹ الذي يتحرك بسرعة ثابتة تساوي v بالنسبة لمحور الاسناد s في اللحظة الزمنية نفسها؟
عند زمن معين، فما هو المجال الكهربائي الذي يقيسه المشاهد في محور الاسناد sʹ الذي يتحرك بسرعة ثابتة تساوي v بالنسبة لمحور الاسناد s في اللحظة الزمنية نفسها؟
وللإجابة على هذا السؤال نأخذ لوحين ساكنين في محور الاسناد s يوازيان المستوى (x, z) كما هو موضح في الشكل (1.1) ونفرض ان شحنة كهربائية مقدارها Q قد تم توزيعها بصورة متجانسة على اللوحين بحيث ان كثافة الشحنة السطحية على احدهما +σ وعلى اللوح الاخر σ-.
مشاهد في محور الاسناد s يمكن ان يقيس شدة المجال الكهربائي باتجاه الاحداثي y فيجده مساويا الى :
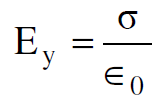 (1.1)
(1.1)
في محور الاسناد sʹ الذي يتحرك بسرعة v باتجاه الاحداثي x الموجب نسبة لمحور الاسناد s نلاحظ ان بعدي اللوحين يلتصقان في هذا الاتجاه بمقدار (1-β2)1/2 حيث ان =v/cβ. وبما ان الشحنة الكلية Q تبقى دون تغيير تحت هذا النوع من التحويلات فان كثافة الشحنة السطحية ʹσ ستزيد على σ بمقدار (1-β2)1/2 اي ان :
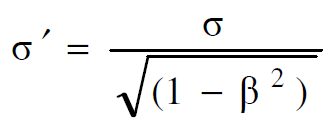 (1.2)
(1.2)
لذا يمكن كتابة المجال الكهربائي Eʹy في محور الاسناد sʹ كالآتي :
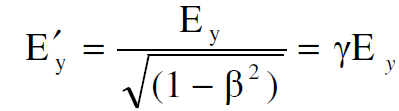 (1.3)
(1.3)
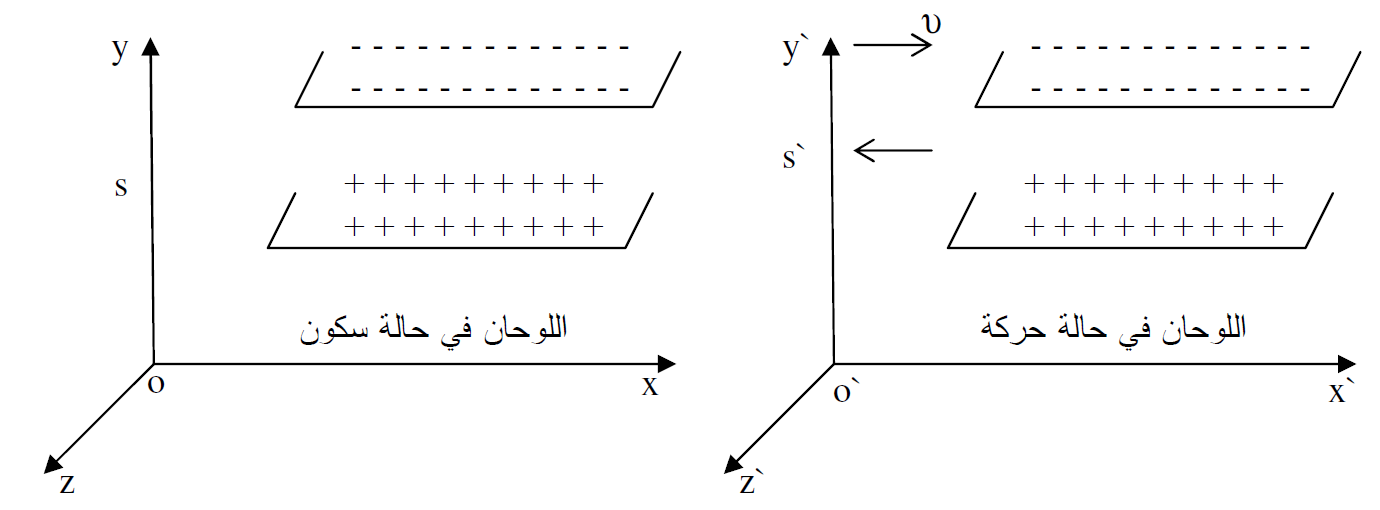
الشكل (1.1) : لوحان متوازيان مشحونان، في حالة سكون موازيان للإحداثي x في s وبنقل الحدث الى sʹ فانهما يتحركان بالاتجاه السالب للإحداثي x.
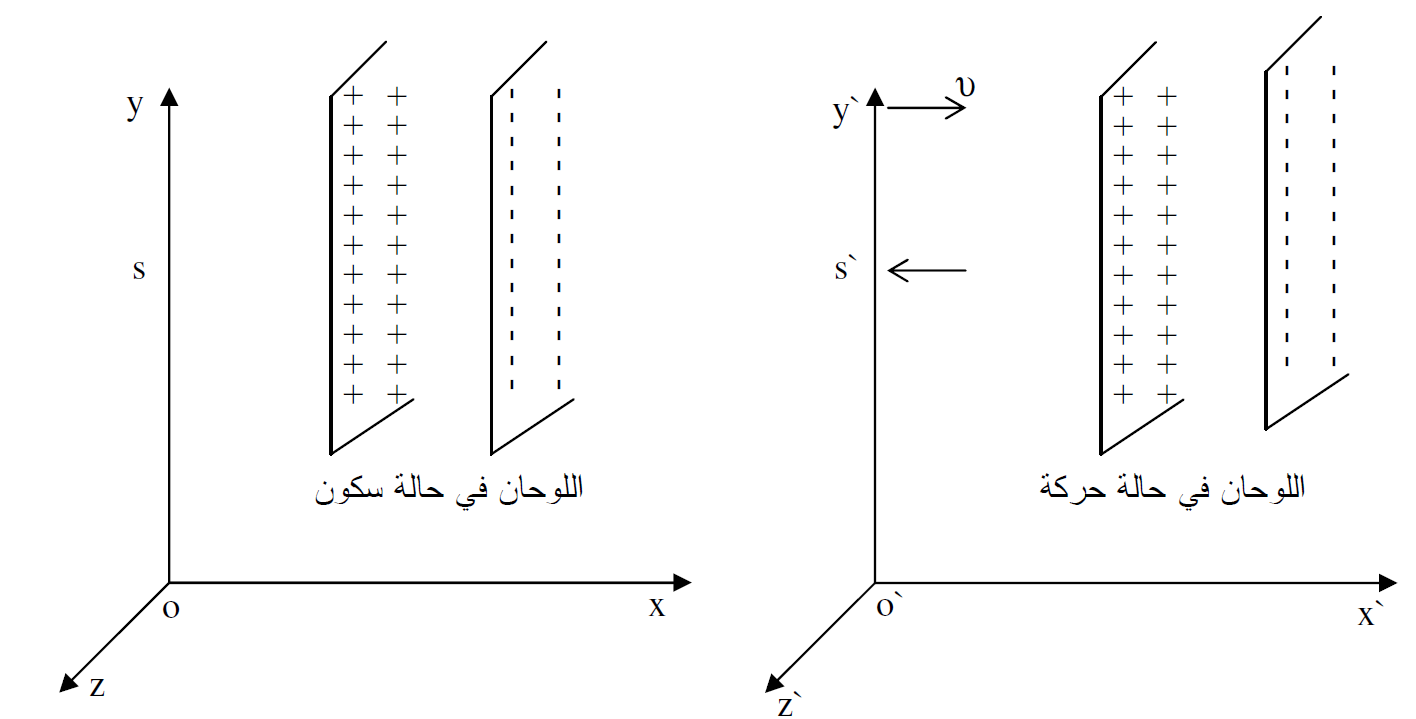
الشكل (1.2) : اللوحان عموديان على الاحداثي x وهما في حالة سكون في s. عندما ينقل الحدث الى sʹ فانهما يتحركان بالاتجاه السالب للإحداثي x.
ولو ناقشنا حالة مختلفة عندما يتعامد اللوحان الساكنان المشحونان على الاحداثي x في محور الاسناد s كما موضح في الشكل (1.2)، فمن الممكن والحالة هذه ان يسجل المشاهد في هذا المحور مجالا كهربائيا باتجاه x مقداره :
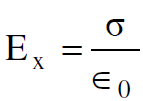 (1.4)
(1.4)
وعندئذ تصبح كثافة الشحنة السطحية الموزعة على اللوحين في محور الاسناد sʹ مساوية تلك في محور الاسناد s لأن بعدي اللوحين لا يحدث لهما تغيير وانما المسافة بينهما هي التي تعاني تغييرا وهذا التغيير لا يدخل في حسابات المجال الكهربائي باتجاه الاحداثي x، لذا فان :
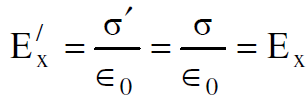 (1.5)
(1.5)
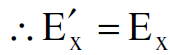 (1.6)
(1.6)
من المعادلتين (1.3) و (1.6) من الممكن صياغة حالة عامة مناسبة للحركة النسبية في اي اتجاه للشحنات الكهربائية الساكنة في محور الاسناد s التي تعتبر مصدرا للمجال الكهربائي 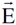 ولنأخذ محور الاسناد sʹ الذي يتحرك بسرعة منتظمة v بالنسبة لمحور الاسناد s ثم نحلل المجال الكهربائي عند أية نقطة في s الى مركبتين : الاولى موازية لاتجاه v وهي EII والاخرى عمودية على اتجاه v وهي E┴.
ولنأخذ محور الاسناد sʹ الذي يتحرك بسرعة منتظمة v بالنسبة لمحور الاسناد s ثم نحلل المجال الكهربائي عند أية نقطة في s الى مركبتين : الاولى موازية لاتجاه v وهي EII والاخرى عمودية على اتجاه v وهي E┴.
وفي نفس اللحظة الزمنية والمكانية نحلل المجال الكهربائي ʹ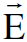 . في محور الاسناد sʹ الى مركبتين ايضا : الاولى موازية لاتجاه v وهي EʹII والاخرى عمودية عليه وهي
. في محور الاسناد sʹ الى مركبتين ايضا : الاولى موازية لاتجاه v وهي EʹII والاخرى عمودية عليه وهي 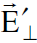 وبالاستعانة بالمعادلتين (1.3) و (1.6) نكتب :
وبالاستعانة بالمعادلتين (1.3) و (1.6) نكتب :
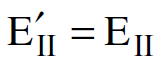 (1.7)
(1.7)
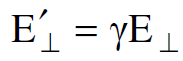 (1.8)
(1.8)
ومن الجدير بالذكر ان المعادلات السابقة تصح للمجالات الكهربائية الناتجة عن الشحنات الكهربائية الساكنة في محور الاسناد s. اما اذا كانت الشحنات الكهربائية متحركة في محور الاسناد s فان المجال في محور الاسناد sʹ لابد ان يتضمن معرفة مجالين في محور الاسناد s وهما المجال الكهربائي والمجال المغناطيسي.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|