The light goes slower in water than in air, and slower, slightly, in air than in vacuum. This effect is described by the index of refraction n. Now we would like to understand how such a slower velocity could come about. In particular, we should try to see what the relation is to some physical assumptions, or statements, we made earlier, which were the following:

1. That the total electric field in any physical circumstance can always be represented by the sum of the fields from all the charges in the universe.
2. That the field from a single charge is given by its acceleration evaluated with a retardation at the speed c, always (for the radiation field).

But, for a piece of glass, you might think: “Oh, no, you should modify all this. You should say it is retarded at the speed c/n.” That, however, is not right, and we have to understand why it is not.

It is approximately true that light or any electrical wave does appear to travel at the speed c/n through a material whose index of refraction is n, but the fields are still produced by the motions of all the charges—including the charges moving in the material—and with these basic contributions of the field travelling at the ultimate velocity c. Our problem is to understand how the apparently slower velocity comes about.

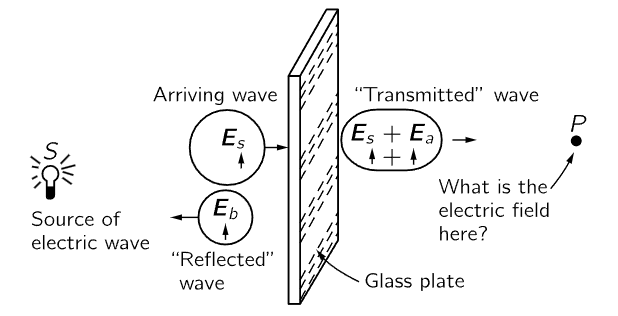
Fig. 31–1. Electric waves passing through a layer of transparent material.

We shall try to understand the effect in a very simple case. A source which we shall call “the external source” is placed a large distance away from a thin plate of transparent material, say glass. We inquire about the field at a large distance on the opposite side of the plate. The situation is illustrated by the diagram of Fig. 31–1, where S and P are imagined to be very far away from the plate. According to the principles we have stated earlier, an electric field anywhere that is far from all moving charges is the (vector) sum of the fields produced by the external source (at S) and the fields produced by each of the charges in the plate of glass, every one with its proper retardation at the velocity c. Remember that the contribution of each charge is not changed by the presence of the other charges. These are our basic principles. The field at P can be written thus:

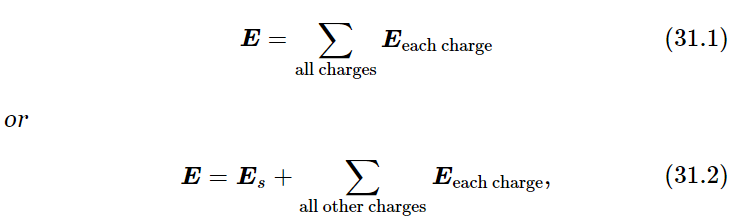
where E_s is the field due to the source alone and would be precisely the field at P if there were no material present. We expect the field at P to be different from E_s if there are any other moving charges.

Why should there be charges moving in the glass? We know that all material consists of atoms which contain electrons. When the electric field of the source acts on these atoms it drives the electrons up and down, because it exerts a force on the electrons. And moving electrons generate a field—they constitute new radiators. These new radiators are related to the source S, because they are driven by the field of the source. The total field is not just the field of the source S, but it is modified by the additional contribution from the other moving charges. This means that the field is not the same as the one which was there before the glass was there, but is modified, and it turns out that it is modified in such a way that the field inside the glass appears to be moving at a different speed. That is the idea which we would like to work out quantitatively.

Now this is, in the exact case, pretty complicated, because although we have said that all the other moving charges are driven by the source field, that is not quite true. If we think of a particular charge, it feels not only the source, but like anything else in the world, it feels all of the charges that are moving. It feels, in particular, the charges that are moving somewhere else in the glass. So, the total field which is acting on a particular charge is a combination of the fields from the other charges, whose motions depend on what this particular charge is doing! You can see that it would take a complicated set of equations to get the complete and exact formula. It is so complicated that we postpone this problem until next year.

Instead, we shall work out a very simple case in order to understand all the physical principles very clearly. We take a circumstance in which the effects from the other atoms are very small relative to the effects from the source. In other words, we take a material in which the total field is not modified very much by the motion of the other charges. That corresponds to a material in which the index of refraction is very close to 1, which will happen, for example, if the density of the atoms is very low. Our calculation will be valid for any case in which the index is for any reason very close to 1. In this way we shall avoid the complications of the most general, complete solution.

Incidentally, you should notice that there is another effect caused by the motion of the charges in the plate. These charges will also radiate waves back toward the source S. This backward-going field is the light we see reflected from the surfaces of transparent materials. It does not come from just the surface. The backward radiation comes from everywhere in the interior, but it turns out that the total effect is equivalent to a reflection from the surfaces. These reflection effects are beyond our approximation at the moment because we shall be limited to a calculation for a material with an index so close to 1 that very little light is reflected.

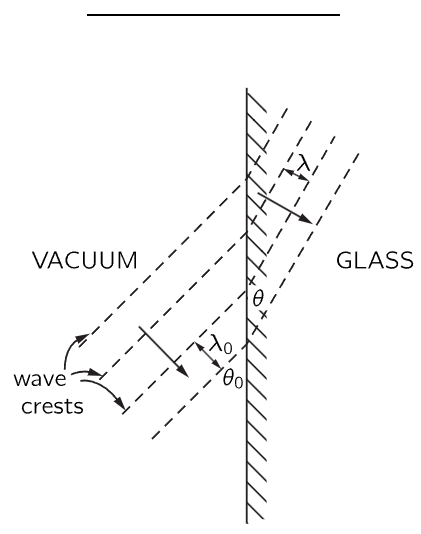
Fig. 31–2. Relation between refraction and velocity change.

Before we proceed with our study of how the index of refraction comes about, we should understand that all that is required to understand refraction is to understand why the apparent wave velocity is different in different materials. The bending of light rays comes about just because the effective speed of the waves is different in the materials. To remind you how that comes about we have drawn in Fig. 31–2 several successive crests of an electric wave which arrives from a vacuum onto the surface of a block of glass. The arrow perpendicular to the wave crests indicates the direction of travel of the wave. Now all oscillations in the wave must have the same frequency. (We have seen that driven oscillations have the same frequency as the driving source.) This means, also, that the wave crests for the waves on both sides of the surface must have the same spacing along the surface because they must travel together, so that a charge sitting at the boundary will feel only one frequency. The shortest distance between crests of the wave, however, is the wavelength which is the velocity divided by the frequency. On the vacuum side it is λ₀=2πc/ω, and on the other side it is λ=2πv/ω or 2πc/ωn, if v=c/n is the velocity of the wave. From the figure we can see that the only way for the waves to “fit” properly at the boundary is for the waves in the material to be travelling at a different angle with respect to the surface. From the geometry of the figure, you can see that for a “fit” we must have λ₀/sinθ₀=λ/sinθ, or sinθ₀/sinθ=n, which is Snell’s law. We shall, for the rest of our discussion, consider only why light has an effective speed of c/n in material of index n, and no longer worry, in this chapter, about the bending of the light direction.

We go back now to the situation shown in Fig. 31–1. We see that what we have to do is to calculate the field produced at P by all the oscillating charges in the glass plate. We shall call this part of the field E_a, and it is just the sum written as the second term in Eq. (31.2). When we add it to the term E_s, due to the source, we will have the total field at P.

This is probably the most complicated thing that we are going to do this year, but it is complicated only in that there are many pieces that have to be put together; each piece, however, is very simple. Unlike other derivations where we say, “Forget the derivation, just look at the answer!” in this case we do not need the answer so much as the derivation. In other words, the thing to understand now is the physical machinery for the production of the index.

To see where we are going, let us first find out what the “correction field” E_a would have to be if the total field at P is going to look like radiation from the source that is slowed down while passing through the thin plate. If the plate had no effect on it, the field of a wave travelling to the right (along the z-axis) would be

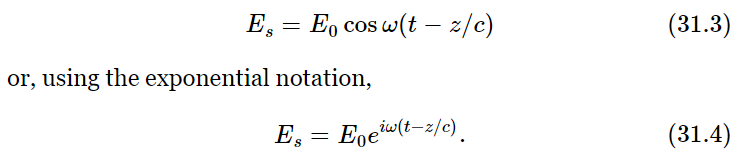
Now what would happen if the wave travelled more slowly in going through the plate? Let us call the thickness of the plate Δz. If the plate were not there the wave would travel the distance Δz in the time Δz/c. But if it appears to travel at the speed c/n then it should take the longer time nΔz/c or the additional time Δt=(n−1) Δz/c. After that it would continue to travel at the speed c again. We can take into account the extra delay in getting through the plate by replacing t in Eq. (31.4) by (t−Δt) or by [t−(n−1) Δz/c]. So, the wave after insertion of the plate should be written

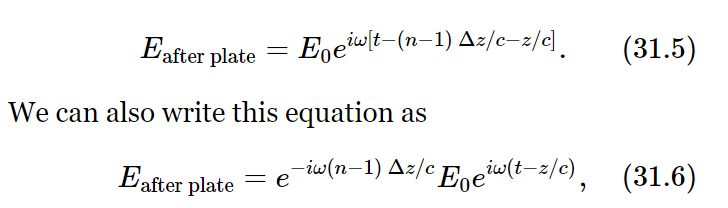
which says that the wave after the plate is obtained from the wave which could exist without the plate, i.e., from E_s, by multiplying by the factor e^{−iω(n−1) Δz/c}. Now we know that multiplying an oscillating function like e^iωt by a factor e^iθ just says that we change the phase of the oscillation by the angle θ, which is, of course, what the extra delay in passing through the thickness Δz has done. It has retarded the phase by the amount ω(n−1) Δz/c (retarded, because of the minus sign in the exponent).

We have said earlier that the plate should add a field E_a to the original field E_s=E₀e^iω(t−z/c), but we have found instead that the effect of the plate is to multiply the field by a factor which shifts its phase. However, that is really all right because we can get the same result by adding a suitable complex number. It is particularly easy to find the right number to add in the case that Δz is small, for you will remember that if x is a small number then e^x is nearly equal to (1+x). We can write, therefore,

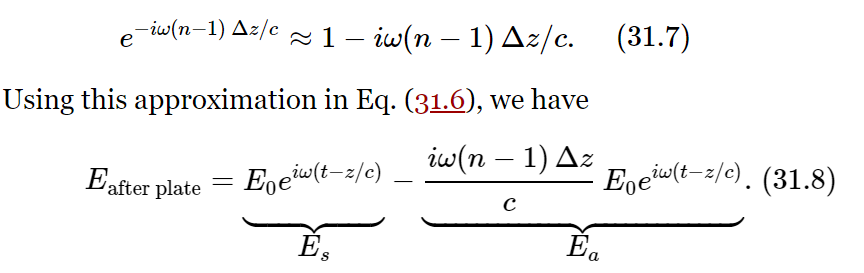
The first term is just the field from the source, and the second term must just be equal to E_a, the field produced to the right of the plate by the oscillating charges of the plate—expressed here in terms of the index of refraction n, and depending, of course, on the strength of the wave from the source.

What we have been doing is easily visualized if we look at the complex number diagram in Fig. 31–3. We first draw the number E_s (we chose some values for z and t so that E_s comes out horizontal, but this is not necessary). The delay due to slowing down in the plate would delay the phase of this number, that is, it would rotate E_s through a negative angle. But this is equivalent to adding the small vector E_a at roughly right angles to E_s. But that is just what the factor −i means in the second term of Eq. (31.8). It says that if E_s is real, then E_a is negative imaginary or that, in general, E_s and E_a make a right angle.

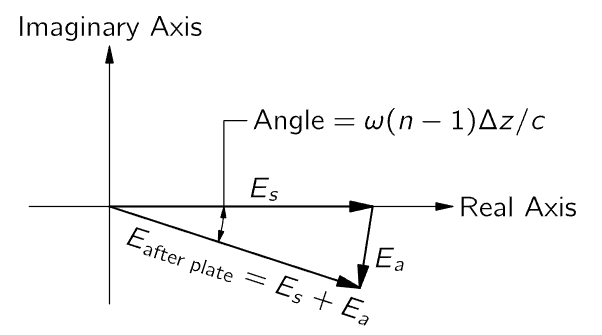
Fig. 31–3. Diagram for the transmitted wave at a particular t and z.