How far, or how big, are things? Everybody knows that the way you measure distance is to start with a stick and count. Or start with a thumb and count. You begin with a unit and count. How does one measure smaller things? How does one subdivide distance? In the same way that we subdivided time: we take a smaller unit and count the number of such units it takes to make up the longer unit. So, we can measure smaller and smaller lengths.

But we do not always mean by distance what one gets by counting off with a meter stick. It would be difficult to measure the horizontal distance between two mountain tops using only a meter stick. We have found by experience that distance can be measured in another fashion: by triangulation. Although this means that we are really using a different definition of distance, when they can both be used, they agree with each other. Space is more or less what Euclid thought it was, so the two types of definitions of distance agree. Since they do agree on the earth it gives us some confidence in using triangulation for still larger distances. For example, we were able to use triangulation to measure the height of the first Sputnik. We found that it was roughly 5×10⁵ meters high. By more careful measurements the distance to the moon can be measured in the same way. Two telescopes at different places on the earth can give us the two angles we need. It has been found in this way that the moon is 4×10⁸ meters away.

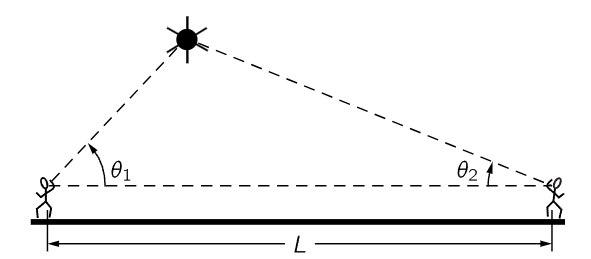
Fig. 5–4. The height of a Sputnik is determined by triangulation.

We cannot do the same with the sun, or at least no one has been able to yet. The accuracy with which one can focus on a given point on the sun and with which one can measure angles is not good enough to permit us to measure the distance to the sun. Then how can we measure the distance to the sun? We must invent an extension of the idea of triangulation. We measure the relative distances of all the planets by astronomical observations of where the planets appear to be, and we get a picture of the solar system with the proper relative distances of everything, but with no absolute distance. One absolute measurement is then required, which has been obtained in a number of ways. One of the ways, which was believed until recently to be the most accurate, was to measure the distance from the earth to Eros, one of the small planetoids which passes near the earth every now and then. By triangulation on this little object, one could get the one required scale measurement. Knowing the relative distances of the rest, we can then tell the distance, for example, from the earth to the sun, or from the earth to Pluto.

Within the past year there has been a big improvement in our knowledge of the scale of the solar system. At the Jet Propulsion Laboratory, the distance from the earth to Venus was measured quite accurately by a direct radar observation. This, of course, is a still different type of inferred distance. We say we know the speed at which light travels (and therefore, at which radar waves travel), and we assume that it is the same speed everywhere between the earth and Venus. We send the radio wave out, and count the time until the reflected wave comes back. From the time we infer a distance, assuming we know the speed. We have really another definition of a measurement of distance.

How do we measure the distance to a star, which is much farther away? Fortunately, we can go back to our triangulation method, because the earth moving around the sun gives us a large baseline for measurements of objects outside the solar system. If we focus a telescope on a star in summer and in winter, we might hope to determine these two angles accurately enough to be able to measure the distance to a star.

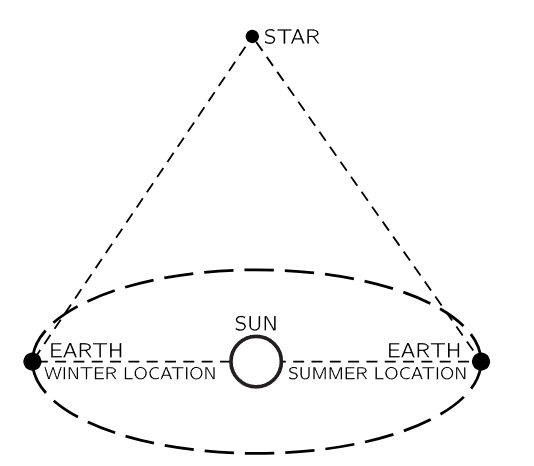
Fig. 5–5. The distance of nearby stars can be measured by triangulation, using the diameter of the earth’s orbit as a baseline.

What if the stars are too far away for us to use triangulation? Astronomers are always inventing new ways of measuring distance. They find, for example, that they can estimate the size and brightness of a star by its color. The color and brightness of many nearby stars—whose distances are known by triangulation—have been measured, and it is found that there is a smooth relationship between the color and the intrinsic brightness of stars (in most cases). If one now measures the color of a distant star, one may use the color-brightness relationship to determine the intrinsic brightness of the star. By measuring how bright the star appears to us at the earth (or perhaps we should say how dim it appears), we can compute how far away it is. (For a given intrinsic brightness, the apparent brightness decreases with the square of the distance.) A nice confirmation of the correctness of this method of measuring stellar distances is given by the results obtained for groups of stars known as globular clusters. A photograph of such a group is shown in Fig. 5–6. Just from looking at the photograph one is convinced that these stars are all together. The same result is obtained from distance measurements by the color-brightness method.

Fig. 5–6. A cluster of stars near the center of our galaxy. Their distance from the earth is 30,000 light-years, or about 3×10²⁰ meters.

A study of many globular clusters gives another important bit of information. It is found that there is a high concentration of such clusters in a certain part of the sky and that most of them are about the same distance from us. Coupling this information with other evidence, we conclude that this concentration of clusters marks the center of our galaxy. We then know the distance to the center of the galaxy—about 10²⁰ meters.

Knowing the size of our own galaxy, we have a key to the measurement of still larger distances—the distances to other galaxies. Figure 5–7 is a photograph of a galaxy, which has much the same shape as our own. Probably it is the same size, too. (Other evidence supports the idea that galaxies are all about the same size.) If it is the same size as ours, we can tell its distance. We measure the angle it subtends in the sky; we know its diameter, and we compute its distance—triangulation again!

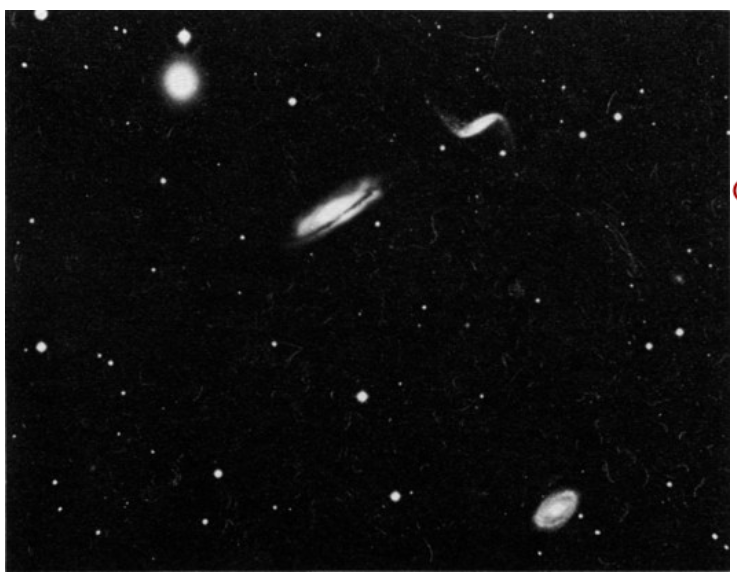
Fig. 5–7.A spiral galaxy like our own. Presuming that its diameter is similar to that of our own galaxy, we may compute its distance from its apparent size. It is 30 million light-years (3×10²³ meters) from the earth.

Photographs of exceedingly distant galaxies have recently been obtained with the giant Palomar telescope. One is shown in Fig. 5–8. It is now believed that some of these galaxies are about halfway to the limit of the universe—10²⁶ meters away—the largest distance we can contemplate!

Fig. 5–8. The most distant object, 3C 295 in Boötes (indicated by the arrow), measured by the 200-inch telescope to date (1960).