
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The Doppler effect
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 34
2024-03-26
1887
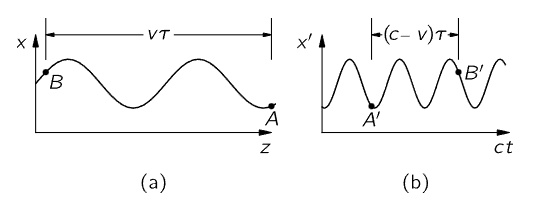
Fig. 34–10. The x-z and x′-t curves of a moving oscillator.
Now we go on to consider some other examples of the effects of moving sources. Let us suppose that the source is a stationary atom which is oscillating at one of its natural frequencies, ω0. Then we know that the frequency of the light we would observe is ω0. But now let us take another example, in which we have a similar oscillator oscillating with a frequency ω1, and at the same time the whole atom, the whole oscillator, is moving along in a direction toward the observer at velocity v. Then the actual motion in space, of course, is as shown in Fig. 34–10(a). Now we play our usual game, we add cτ; that is to say, we translate the whole curve backward and we find then that it oscillates as in Fig. 34–10(b). In a given amount of time τ, when the oscillator would have gone a distance vτ, on the x′ vs. ct diagram it goes a distance (c−v) τ. So, all the oscillations of frequency ω1 in the time Δτ are now found in the interval Δt=(1−v/c) Δτ; they are squashed together, and as this curve comes by us at speed c, we will see light of a higher frequency, higher by just the compression factor (1−v/c). Thus, we observe

We can, of course, analyze this situation in various other ways. Suppose that the atom were emitting, instead of sine waves, a series of pulses, pip, pip, pip, pip, at a certain frequency ω1. At what frequency would they be received by us? The first one that arrives has a certain delay, but the next one is delayed less because in the meantime the atom moves closer to the receiver. Therefore, the time between the “pips” is decreased by the motion. If we analyze the geometry of the situation, we find that the frequency of the pips is increased by the factor 1/(1−v/c).
Is ω=ω0/(1−v/c), then, the frequency that would be observed if we took an ordinary atom, which had a natural frequency ω0, and moved it toward the receiver at speed v? No; as we well know, the natural frequency ω1 of a moving atom is not the same as that measured when it is standing still, because of the relativistic dilation in the rate of passage of time. Thus if ω0 were the true natural frequency, then the modified natural frequency ω1 would be
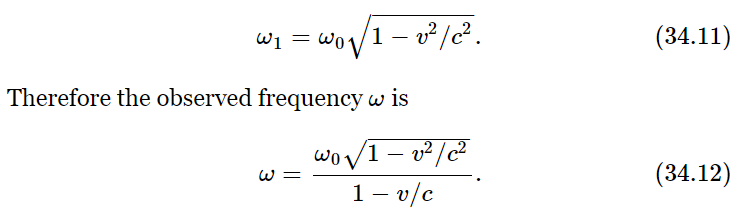
The shift in frequency observed in the above situation is called the Doppler effect: if something moves toward us the light it emits appears more violet, and if it moves away it appears more red.
We shall now give two more derivations of this same interesting and important result. Suppose, now, that the source is standing still and is emitting waves at frequency ω0, while the observer is moving with speed v toward the source. After a certain period of time t the observer will have moved to a new position, a distance vt from where he was at t=0. How many radians of phase will he have seen go by? A certain number, ω0t, went past any fixed point, and in addition the observer has swept past some more by his own motion, namely a number vtk0 (the number of radians per meter times the distance). So, the total number of radians in the time t, or the observed frequency, would be ω1=ω0+k0v. We have made this analysis from the point of view of a man at rest; we would like to know how it would look to the man who is moving. Here we have to worry again about the difference in clock rate for the two observers, and this time that means that we have to divide by 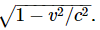 So if k0 is the wave number, the number of radians per meter in the direction of motion, and ω0 is the frequency, then the observed frequency for a moving man is
So if k0 is the wave number, the number of radians per meter in the direction of motion, and ω0 is the frequency, then the observed frequency for a moving man is
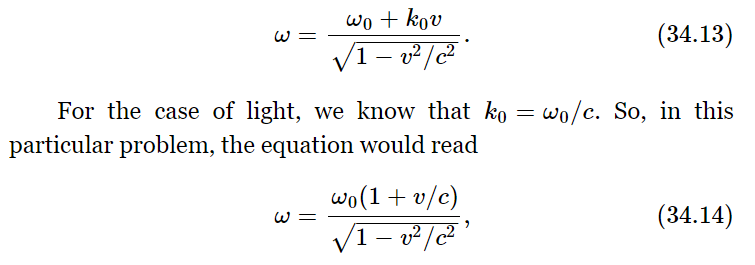
which looks completely unlike formula (34.12)! Is the frequency that we would observe if we move toward a source different than the frequency that we would see if the source moved toward us? Of course not! The theory of relativity says that these two must be exactly equal. If we were expert enough mathematicians, we would probably recognize that these two mathematical expressions are exactly equal! In fact, the necessary equality of the two expressions is one of the ways by which some people like to demonstrate that relativity requires a time dilation, because if we did not put those square-root factors in, they would no longer be equal.
Since we know about relativity, let us analyze it in still a third way, which may appear a little more general. (It is really the same thing, since it makes no difference how we do it!) According to the relativity theory there is a relationship between position and time as observed by one man and position and time as seen by another who is moving relative to him. We wrote down those relationships long ago (Chapter 16). This is the Lorentz transformation and its inverse:
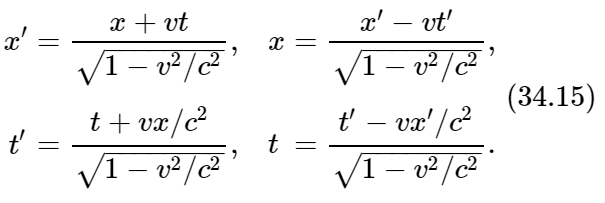
If we were standing still on the ground, the form of a wave would be cos(ωt−kx); all the nodes and maxima and minima would follow this form. But what would a man in motion, observing the same physical wave, see? Where the field is zero, the positions of all the nodes are the same (when the field is zero, everyone measures the field as zero); that is a relativistic invariant. So the form is the same for the other man too, except that we must transform it into his frame of reference:
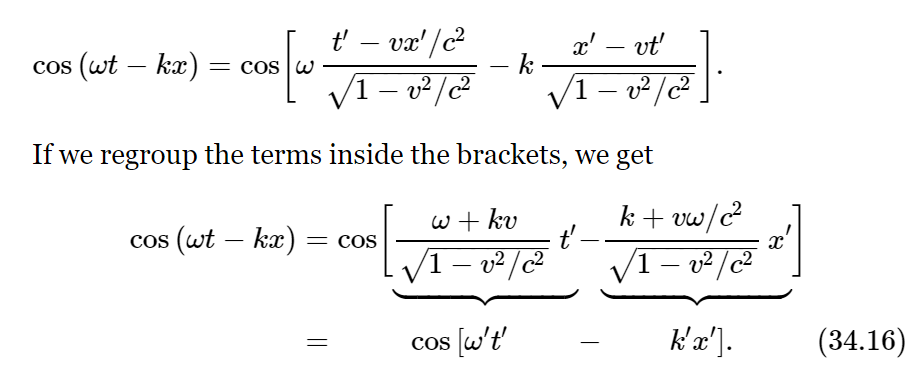
This is again a wave, a cosine wave, in which there is a certain frequency ω′, a constant multiplying t′, and some other constant, k′, multiplying x′. We call k′ the wave number, or the number of waves per meter, for the other man. Therefore, the other man will see a new frequency and a new wave number given by
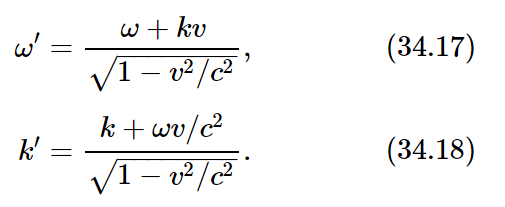
If we look at (34.17), we see that it is the same formula (34.13), that we obtained by a more physical argument.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















