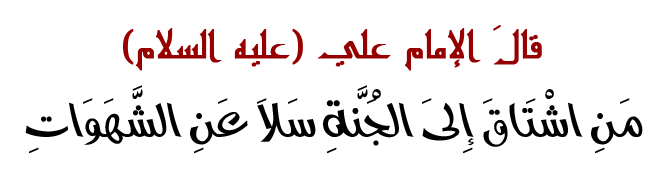
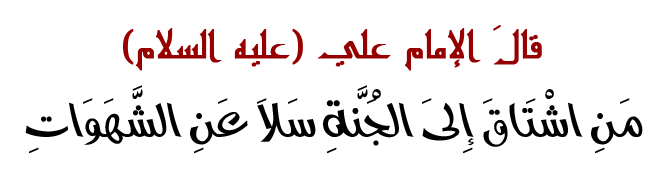

 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2015
Date: 21-10-2015
Date: 15-10-2015
|
Born: 950 in Egypt
Died: 1009 in Fustat, Egypt
Ibn Yunus's full name is Abu'l-Hasan Ali ibn Abd al-Rahman ibn Ahmad ibn Yunus al-Sadafi. As the name indicates, his great-grandfather was called Yunus, his grandfather was Ahmad, and his father Abd al-Rahman. It was a family of scholars, his father Abd al-Rahman being a noted historian.
We know little of ibn Yunus's childhood but we do know that he grew up in a period of military conquest in Egypt. The Fatimid political and religious dynasty took its name from Fatimah, the daughter of the Prophet Muhammad. The Fatimids headed a religious movement dedicated to taking over the whole of the political and religious world of Islam. As a consequence they refused to recognise the 'Abbasid caliphs. The Fatimid caliphs ruled North Africa and Sicily during the first half of the 10th century, but after a number of unsuccessful attempts to defeat Egypt, they began a major advance into that country in 969 conquering the Nile Valley. They founded the city of Cairo as the capital of their new empire.
Ibn Yunus was closely connected with the Fatimids and two Caliphs supported his scientific work. The first of these Caliphs was al-Aziz, who was the first of the Fatimid caliphs to begin his reign in Egypt. Al-Aziz became Caliph in 975 on the death of his father al-Mu'izz and, two years later, ibn Yunus began to make astronomical observations. Although there is uncertainty about the instruments that ibn Yunus used, it is claimed by early writers that al-Aziz provided ibn Yunus with at least some instruments.
Famed for his astronomical observations, ibn Yunus was also an astrologer but he is most famous for his many trigonometrical and astronomical tables. Of course it was very reasonable for a Caliph to support the type of astronomical work that ibn Yunus was undertaking. The Muslim religion required considerable knowledge of the moon and the sun to determine the times of prayer during the year. The Muslin lunar calendar required that the new months be determined by actual visibility of the lunar crescent rather than duration of the lunar month, so it was necessary to know a number of different details such as how far the moon was from the sun to determine when it became visible.
Perhaps al-Aziz would have given better support to ibn Yunus if he had not been so involved in military and political ventures in northern Syria trying to expand the Fatimid empire. For most of his 20 year reign he worked towards this aim while ibn Yunus toiled on his astronomical work. Al-Aziz died in 996 while organising an army to march against the Byzantines and al-Hakim, who was eleven years old at the time, became Caliph. We should note, however, that in [5] the author suggests that Yunus probably had the use of professional calculators in preparing his tables so perhaps al-Aziz or al-Hakim gave him more support than we have suggested above.
Certainly al-Hakim supported ibn Yunus in his astronomical work, although it is hard to determine the strength of that support. Perhaps al-Hakim's interest in astrology meant that he favoured ibn Yunus who is reported by his biographers to have devoted considerable amounts of time to making astrological predictions. Ibn Yunus and al-Hakim were both eccentrics, although al-Hakim's eccentricities were more damaging, while ibn Yunus's sound rather typical of someone totally absorbed in academic pursuits.
Ibn Yunus was described by his biographer al-Musabbihi, who was a contemporary of ibn Yunus, as follows (see [1]):-
He was an eccentric, careless and absent-minded man who dressed shabbily and had a comic appearance.
On the other hand al-Hakim ordered the sacking of the city al-Fustat, the city in which ibn Yunus sometimes observed from his great-grandfather's house. Al-Hakim ordered the killing of all dogs, since their barking annoyed him, and he banned certain vegetables and shellfish. However, probably because of his interest in astrology, al-Hakim kept some astronomical instruments in his house overlooking Cairo and we know that on at least one occasion ibn Yunus observed Venus from al-Hakim's house.
Ibn Yunus's major work, an astronomical handbook, was al-Zij al-Hakimi al-kabir. 'Al-kabir' means 'large' which is apt and 'al-Hakimi' means that the work is dedicated to Caliph al-Hakim who certainly supported ibn Yunus. The book is certainly large, containing 81 chapters. There are lists of observations made by Yunus and also observations made by his predecessors. In fact it is a rather remarkable fact that singles the work out from all similar works of that period. Other authors never distinguished between their observations and those in their works which had been made by other scientists.
He describes 40 planetary conjunctions accurately and 30 lunar eclipses which were used by Simon Newcomb in his lunar theory. To give an example of a planetary conjunction described in the Hakimi Zij we quote from [2] (see also [1]) having changed the dates given by ibn Yunus to those of a modern calendar:-
A conjunction of Venus and Mercury in Gemini, observed in the western sky: The two planets were in conjunction after sunset on the night [of Sunday 19 May 1000]. The time was approximately eight equinoctial hours after midday on Sunday ... . Mercury was north of Venus and their latitude difference was a third of a degree.
We can confirm, using modern knowledge of the positions of the planets, that ibn Yunus was exactly right in his description and that the distance of one third of a degree that he gives is again exactly right. He also describes an eclipse of the moon [2]:-
This lunar eclipse was [on 22 April 981]. We gathered to observe this eclipse at al-Qarafa, in the Mosque of Ibn Nasr al Maghribi. We perceived first contact when the altitude of the moon was approximately 21°. About a quarter of the lunar diameter was eclipsed, and reemergence occurred about a quarter of an hour before sunrise.
The first chapter of the Hakimi Zij gives calendar tables for Muslim, Coptic, Syrian and Persian calendars. Ibn Yunus gives tables to convert dates between these calendars. Tables to compute the date of Easter are also given. Trigonometric functions are given as arcs rather than angles. Spherical trigonometry reaches a high level of sophistication in this work.
Many other tables have been attriributed to ibn Yunus. For example in [9] the author writes:-
In this paper I describe a set of tables for finding the longitude of the moon, attributed to the tenth century Egyptian astonomer ibn Yunus. The underlying lunar theory is that of Ptolemy, but these tables are so devised that the user is spared the calculations which are associated with Ptolemy's lunar tables. Ibn Yunus's tables, if such they are, contain over 34000 entries ... . The tables are of interest as the earliest attempt by a medieval scholar to solve the computational problem of the determination of the lunar position according to the sophisticated Ptolemaic theory.
In [5] ibn Yunus's Very useful tables for finding the time since sunrise, the hour angle and the solar azimuth from the solar altitude are described. The author notes that ibn Yunus used data for these tables that he had collected for the Hakimi Zij. The high degree of accuracy displayed by these tables suggests to D A King that ibn Yunus used systems of nonlinear interpolation.
Perhaps it is worth mentioning that, contrary to claims which are often made, there is no evidence to suggest that ibn Yunus used a pendulum for time measurements. D A King in [8] shows that this myth was started in 1684 by the English historian Edward Bernard.
Ibn Yunus predicted the date of his own death to be in seven days time when he was in good health. He tidied up his business affairs, locked himself in his house and recited the Qur'an until he died on the day he predicted.
Articles:



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|