المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
السلام عليك يا داعيَ الله وربانيَّ آياته
2025-04-07
سلامٌ على آل ياسين
2025-04-07
التوجه إلى الله بأهل البيت ( عليهم السلام ) والتوجه إليهم
2025-04-07
تفريعات / القسم الثاني عشر
2025-04-06
تفريعات / القسم الحادي عشر
2025-04-06
تفريعات / القسم العاشر
2025-04-06

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
تكرارية الطفرات في فايروسات النبات وسرعتها
3-9-2017
التقييم القانوني لمعاهدة عام 1913الخاصة بترسيم الحدود العراقية
23-3-2017
Modules-Tensor Products of Bimodules
4-7-2017
عقوبة جريمة هتك العرض
2024-10-06
التكتيكات
1/9/2022
أنماط حصول التعلم والاكتساب
26-7-2016

Durand,s Rule  
  
509   06:32 مساءً   date: 2-12-2021
Author : Beyer, W. H. (Ed.)
Book or Source : CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press
Page and Part : p. 127


Read More
Polynomial Roots
Date: 14-12-2021 1498
Hardy,s Rule
Date: 5-12-2021 582
Schröder,s Method
Date: 14-12-2021 1295

Durand's Rule

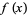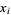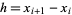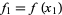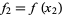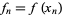Let the values of a function f(x) be tabulated at points x_i equally spaced by h=x_(i+1)-x_i, so f_1=f(x_1), f_2=f(x_2), ..., f_n=f(x_n). Then Durand's rule approximating the integral of 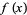f(x) is given by the Newton-Cotes-like formula

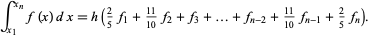int_(x_1)^(x_n)f(x)dx=h(2/5f_1+(11)/(10)f_2+f_3+...+f_(n-2)+(11)/(10)f_(n-1)+2/5f_n).

REFERENCES:

Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 127, 1987.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
التاريخ / 2025-04-04

الأخبار العلمية
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
التاريخ / 2025-04-04

الساحة الاسلامية
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
التاريخ / 2025-04-06