المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Muller,s Method |
 1033
 04:15 مساءً
date: 21-11-2021 |
Author : Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. 
Book or Source : Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press 
Page and Part : p. 364|
Read More
Date: 29-9-2021
1088
Date: 11-2-2016
1323
Date: 10-11-2021
657
|
Generalizes the secant method of root finding by using quadratic 3-point interpolation
 |
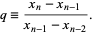(1) |
Then define
 |
 |
 |
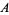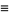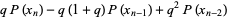(2) |
 |
 |
 |
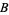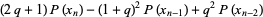(3) |
 |
 |
 |
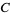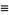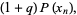(4) |
and the next iteration is
 |
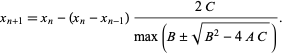(5) |
This method can also be used to find complex zeros of analytic functions.
REFERENCES:
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 364, 1992.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
جمعية العميد تعقد اجتماعًا لمناقشة المشاريع العلمية والبحثية
|
|
|
