Quotient Vector Space

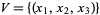Suppose that  and 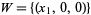. Then the quotient space  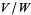(read as " 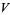mod 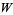") is isomorphic to .

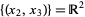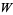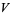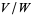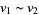In general, when  is a subspace of a vector space , the quotient space  is the set of equivalence classes  where  if 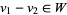. By " 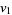is equivalent to  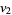modulo 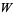," it is meant that  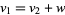for some  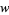in 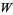, and is another way to say 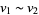. In particular, the elements of  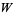represent . Sometimes the equivalence classes  are written as cosets .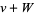

The quotient space is an abstract vector space, not necessarily isomorphic to a subspace of 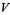. However, if  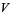has an inner product, then  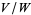is isomorphic to

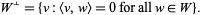In the example above, .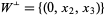

Unfortunately, a different choice of inner product can change 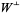. Also, in the infinite-dimensional case, it is necessary for  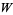to be a closed subspace to realize the isomorphism between  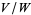and 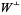, as well as to ensure the quotient space is a T2-space.