


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2021
Date: 14-8-2021
Date: 15-6-2021
|
Let 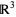 be the space in which a knot
be the space in which a knot 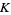 sits. Then the space "around" the knot, i.e., everything but the knot itself, is denoted
sits. Then the space "around" the knot, i.e., everything but the knot itself, is denoted 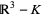 and is called the knot complement of
and is called the knot complement of 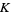 (Adams 1994, p. 84).
(Adams 1994, p. 84).
If a knot complement is hyperbolic (in the sense that it admits a complete Riemannian metric of constant Gaussian curvature 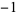 ), then this metric is unique (Prasad 1973, Hoste et al. 1998).
), then this metric is unique (Prasad 1973, Hoste et al. 1998).
REFERENCES:
Adams, C. C. "Knot Complements and Three-Manifolds." §9.1 in The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 243-246, 1994.
Cipra, B. "To Have and Have Knot: When are Two Knots Alike?" Science 241, 1291-1292, 1988.
Gordon, C. and Luecke, J. "Knots are Determined by their Complements." J. Amer. Math. Soc. 2, 371-415, 1989.
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 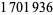 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Prasad, G. "Stong Rigidity of 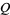 -Rank 1 Lattices." Invent. Math. 21, 255-286, 1973.
-Rank 1 Lattices." Invent. Math. 21, 255-286, 1973.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, 1976.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|