


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-7-2021
Date: 16-7-2021
Date: 14-8-2021
|
Let 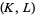 be a pair consisting of finite, connected CW-complexes where
be a pair consisting of finite, connected CW-complexes where 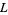 is a subcomplex of
is a subcomplex of 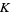 . Define the associated chain complex
. Define the associated chain complex 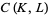 group-wise for each
group-wise for each 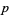 by setting
by setting
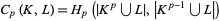 |
(1) |
where 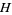 denotes singular homology with integer coefficients and where
denotes singular homology with integer coefficients and where 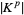 denotes the union of all cells of
denotes the union of all cells of 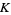 of dimension less than or equal to
of dimension less than or equal to 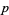 . Note that
. Note that 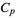 is free Abelian with one generator for each
is free Abelian with one generator for each 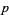 -cell of
-cell of 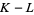 .
.
Next, consider the universal covering complexes 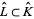 of
of 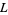 and
and 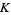 , respectively. The fundamental group
, respectively. The fundamental group 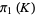 of
of 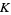 can be identified with the group of deck transformations of
can be identified with the group of deck transformations of 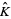 so that each
so that each 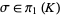 determines a map
determines a map
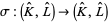 |
(2) |
which then induces a chain map
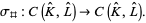 |
(3) |
The chain map 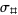 turns each chain group
turns each chain group 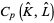 into a module over the group ring
into a module over the group ring 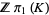 which is
which is 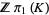 -free with one generator for each
-free with one generator for each 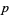 -cell of
-cell of 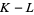 and which is finitely generated over
and which is finitely generated over 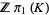 due to the finiteness of
due to the finiteness of 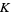 .
.
Hence, there is a free chain complex
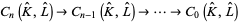 |
(4) |
over 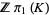 , the homology groups
, the homology groups 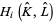 of which are zero due to the fact that
of which are zero due to the fact that 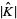 deformation retracts onto
deformation retracts onto 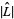 . A simple argument shows the existence of a so-called preferred basis for each
. A simple argument shows the existence of a so-called preferred basis for each 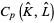 (Milnor), whereby one can define the Whitehead torsion to be the image of the torsion
(Milnor), whereby one can define the Whitehead torsion to be the image of the torsion 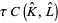 of the complex
of the complex 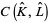 in the Whitehead quotient group
in the Whitehead quotient group 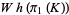 .
.
Worth noting is that the Whitehead torsion is an obvious generalization of the Reidemeister torsion, the prior of which is defined to be an Abelian group element rather than an algebraic number like the latter. Experts note that the study of Reidemeister torsion has since been subsumed in the study of Whitehead torsion (Ranicki 1997) whereas Whitehead torsion provides a fundamental tool for the examination of differentiable and combinatorial manifolds having nontrivial fundamental group.
REFERENCES:
Milnor, J. "Whitehead Torsion." Bull. Amer. Math. Soc. 72, 358-423, 1966.
Ranicki, A. "Notes on Reidemeister Torsion." 1997. https://www.maths.ed.ac.uk/~aar/papers/torsion.pdf.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|