


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-4-2021
Date: 7-2-2021
Date: 7-4-2021
|
A random process consisting of a sequence of discrete steps of fixed length. The random thermal perturbations in a liquid are responsible for a random walk phenomenon known as Brownian motion, and the collisions of molecules in a gas are a random walk responsible for diffusion. Random walks have interesting mathematical properties that vary greatly depending on the dimension in which the walk occurs and whether it is confined to a lattice.
REFERENCES:
Barber, M. N. and Ninham, B. W. Random and Restricted Walks: Theory and Applications. New York: Gordon and Breach, 1970.
Chandrasekhar, S. In Selected Papers on Noise and Stochastic Processes (Ed. N. Wax). New York: Dover, 1954.
Doyle, P. G. and Snell, J. L. Random Walks and Electric Networks. Washington, DC: Math. Assoc. Amer, 1984.
Dykin, E. B. and Uspenskii, V. A. Random Walks. New York: Heath, 1963.
Erdős, P. and Révész, P. "Three Problems on the Random Walk in 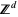 ." Studia Sci. Math. Hung. 26, 309-320, 1991.
." Studia Sci. Math. Hung. 26, 309-320, 1991.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, 1971.
Gardner, M. "Random Walks and Gambling" and "Random Walks on the Plane and in Space." Chs. 6-7 in Mathematical Circus: More Puzzles, Games, Paradoxes, and Other Mathematical Entertainments. Washington, DC: Math. Assoc. Amer., pp. 66-86, 1992.
Hughes, B. D. Random Walks and Random Environments, Vol. 1: Random Walks. New York: Oxford University Press, 1995.
Hughes, B. D. Random Walks and Random Environments, Vol. 2: Random Environments. New York: Oxford University Press, 1996.
Lawler, G. F. Intersections of Random Walks. Boston, MA: Birkhäuser, 1996.
Révész, P. Random Walks in Random and Non-Random Environments. Singapore: World Scientific, 1990.
Spitzer, F. Principles of Random Walk, 2nd ed. New York: Springer-Verlag, 1976.
Weiss, G. Aspects and Applications of the Random Walk. Amsterdam, Netherlands: North-Holland, 1994.
Weisstein, E. W. "Books about Random Walks." https://www.ericweisstein.com/encyclopedias/books/RandomWalks.html.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|