
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-3-2021
Date: 28-2-2021
Date: 4-5-2021
|
The inverse Gaussian distribution, also known as the Wald distribution, is the distribution over 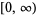 with probability density function and distribution function given by
with probability density function and distribution function given by
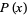 |
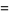 |
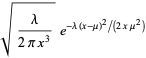 |
(1) |
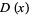 |
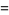 |
![1/2{1+erf[sqrt(lambda/(2x))(x/mu-1)]}+1/2e^(2lambda/mu){1-erf[sqrt(lambda/(2x))(x/mu+1)]},](https://mathworld.wolfram.com/images/equations/InverseGaussianDistribution/Inline7.gif) |
(2) |
where 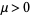 is the mean and
is the mean and 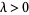 is a scaling parameter.
is a scaling parameter.
The inverse Gaussian distribution is implemented in the Wolfram Language as InverseGaussianDistribution[mu, lambda].
The 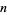 th raw moment is given by
th raw moment is given by
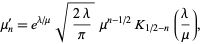 |
(3) |
where 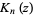 is a modified Bessel function of the second kind, giving the first few as
is a modified Bessel function of the second kind, giving the first few as
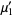 |
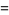 |
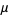 |
(4) |
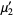 |
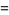 |
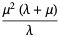 |
(5) |
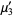 |
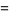 |
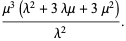 |
(6) |
Using 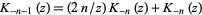 gives a recursion relation for the raw moments as
gives a recursion relation for the raw moments as
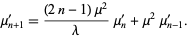 |
(7) |
The first few central moments are
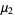 |
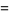 |
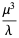 |
(8) |
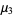 |
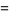 |
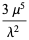 |
(9) |
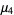 |
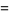 |
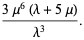 |
(10) |
The cumulants 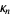 are given by
are given by
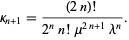 |
(11) |
The variance, skewness, and kurtosis excess are given by
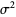 |
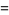 |
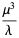 |
(12) |
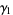 |
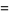 |
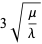 |
(13) |
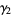 |
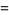 |
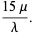 |



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|