


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-3-2021
Date: 28-2-2021
Date: 27-3-2021
|
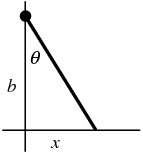
The Cauchy distribution, also called the Lorentzian distribution or Lorentz distribution, is a continuous distribution describing resonance behavior. It also describes the distribution of horizontal distances at which a line segment tilted at a random angle cuts the x-axis.
Let 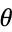 represent the angle that a line, with fixed point of rotation, makes with the vertical axis, as shown above. Then
represent the angle that a line, with fixed point of rotation, makes with the vertical axis, as shown above. Then
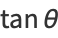 |
 |
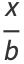 |
(1) |
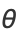 |
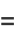 |
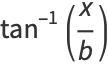 |
(2) |
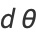 |
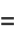 |
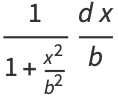 |
(3) |
 |
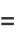 |
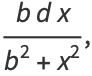 |
(4) |
so the distribution of angle 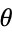 is given by
is given by
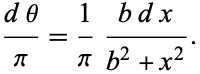 |
(5) |
This is normalized over all angles, since
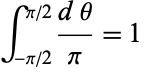 |
(6) |
and
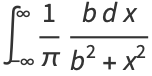 |
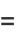 |
![1/pi[tan^(-1)(x/b)]_(-infty)^infty](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline17.gif) |
(7) |
 |
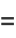 |
![1/pi[1/2pi-(-1/2pi)]](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline20.gif) |
(8) |
 |
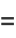 |
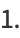 |
(9) |
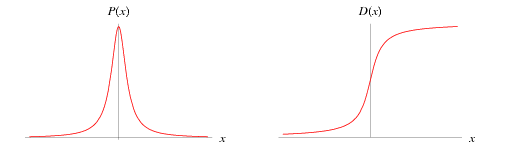
The general Cauchy distribution and its cumulative distribution can be written as
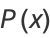 |
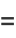 |
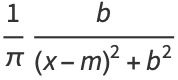 |
(10) |
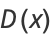 |
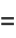 |
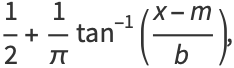 |
(11) |
where 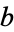 is the half width at half maximum and
is the half width at half maximum and 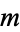 is the statistical median. In the illustration about,
is the statistical median. In the illustration about, 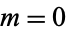 .
.
The Cauchy distribution is implemented in the Wolfram Language as CauchyDistribution[m, Gamma/2].
The characteristic function is
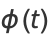 |
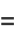 |
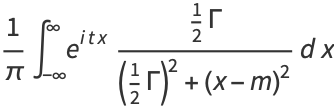 |
(12) |
 |
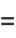 |
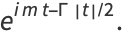 |
(13) |
The moments 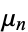 of the distribution are undefined since the integrals
of the distribution are undefined since the integrals
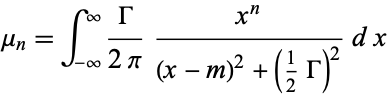 |
(14) |
diverge for 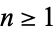 .
.
If 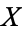 and
and 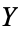 are variates with a normal distribution, then
are variates with a normal distribution, then 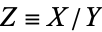 has a Cauchy distribution with statistical median
has a Cauchy distribution with statistical median 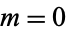 and full width
and full width
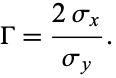 |
(15) |
The sum of 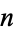 variates each from a Cauchy distribution has itself a Cauchy distribution, as can be seen from
variates each from a Cauchy distribution has itself a Cauchy distribution, as can be seen from
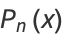 |
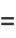 |
![F_t^(-1){[phi(t)]^n}(x)](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline48.gif) |
(16) |
 |
 |
![((1/2nGamma))/(pi[(1/2nGamma)^2+(x-nm)^2]),](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline51.gif) |
(17) |
where 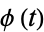 is the characteristic function and
is the characteristic function and ](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline53.gif) is the inverse Fourier transform, taken with parameters
is the inverse Fourier transform, taken with parameters 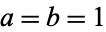 .
.
REFERENCES:
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 104, 1984.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 114-115, 1992.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|