


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-12-2020
Date: 5-11-2020
Date: 1-10-2020
|
The integer sequence beginning with a single digit in which the next term is obtained by describing the previous term. Starting with 1, the sequence would be defined by "1, one 1, two 1s, one 2 one 1," etc., and the result is 1, 11, 21, 1211, 111221, .... Similarly, starting the sequence instead with the digit 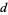 for
for 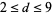 gives
gives 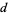 , 1
, 1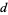 , 111
, 111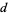 , 311
, 311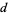 , 13211
, 13211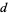 , 111312211
, 111312211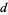 , 31131122211
, 31131122211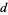 , 1321132132211
, 1321132132211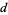 , ..., as summarized in the following table.
, ..., as summarized in the following table.
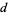 |
OEIS | sequence |
| 1 | A005150 | 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... |
| 2 | A006751 | 2, 12, 1112, 3112, 132112, 1113122112, 311311222112, ... |
| 3 | A006715 | 3, 13, 1113, 3113, 132113, 1113122113, 311311222113, ... |
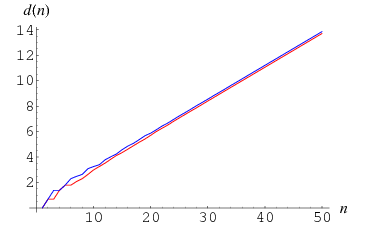
The number of digits in the 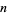 th term of the sequence for
th term of the sequence for 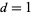 are 1, 2, 2, 4, 6, 6, 8, 10, 14, 20, 26, 34, 46, 62, ... (OEIS A005341). Similarly, the numbers of digits for the
are 1, 2, 2, 4, 6, 6, 8, 10, 14, 20, 26, 34, 46, 62, ... (OEIS A005341). Similarly, the numbers of digits for the 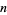 th term of the sequence for
th term of the sequence for 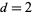 , 3, ..., are 1, 2, 4, 4, 6, 10, 12, 14, 22, 26, ... (OEIS A022471). These sequences are asymptotic to
, 3, ..., are 1, 2, 4, 4, 6, 10, 12, 14, 22, 26, ... (OEIS A022471). These sequences are asymptotic to 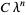 , where
, where
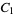 |
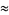 |
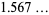 |
(1) |
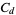 |
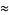 |
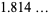 |
(2) |
 |
 |
 |
(3) |
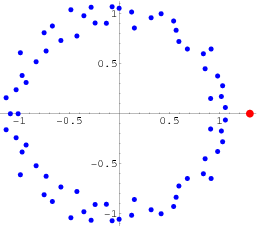
The quantity 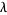 is known as Conway's constant (OEIS A014715), and amazingly is given by the unique positive real root of the polynomial
is known as Conway's constant (OEIS A014715), and amazingly is given by the unique positive real root of the polynomial
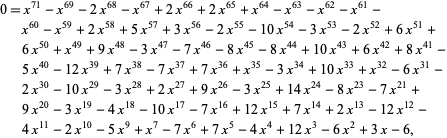 |
(4) |
all of whose roots are illustrated above.
In fact, the constant is even more general than this, applying to all starting sequences (i.e., even those starting with arbitrary starting digits), with the exception of 22, a result which follows from the cosmological theorem. Conway discovered that strings sometimes factor as a concatenation of two strings whose descendants never interfere with one another. A string with no nontrivial splittings is called an "element," and other strings are called "compounds." It is postulated that every string of 1s, 2s, and 3s that does not contain four of the same number in succession eventually "decays" into a compound of 92 special elements, named after the chemical elements.
REFERENCES:
Conway, J. H. "The Weird and Wonderful Chemistry of Audioactive Decay." Eureka 46, 5-18, 1986.
Conway, J. H. "The Weird and Wonderful Chemistry of Audioactive Decay." §5.11 in Open Problems in Communications and Computation. (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 173-188, 1987.
Conway, J. H. and Guy, R. K. "The Look and Say Sequence." In The Book of Numbers. New York: Springer-Verlag, pp. 208-209, 1996.
Hilgemeier, M. "Die Gleichniszahlen-Reihe." Bild der Wissensch. 12, 194-196, Dec. 1986.
Hilgemeier, M. "'One Metaphor Fits All': A Fractal Voyage with Conway's Audioactive Decay." Ch. 7 in Pickover, C. A. (Ed.). Fractal Horizons: The Future Use of Fractals. New York: St. Martin's Press, 1996.
Pickover, C. A. "Audioactive Decay." Ch. 55 in Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, pp. 134-138, 2001.
Sloane, N. J. A. Sequences A005150/M4780, A005341/M0321, A006715/M2965, and A006751/M2052 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 13-14, 1991.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 905, 2002.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
خدمات متعددة يقدمها قسم الشؤون الخدمية للزائرين
|
|
|