


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2020
Date: 1-12-2019
Date: 13-1-2021
|
Consider decomposition the factorial 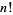 into multiplicative factors
into multiplicative factors 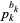 arranged in nondecreasing order. For example,
arranged in nondecreasing order. For example,
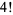 |
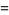 |
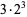 |
(1) |
 |
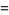 |
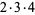 |
(2) |
 |
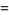 |
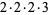 |
(3) |
and
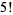 |
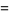 |
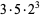 |
(4) |
 |
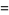 |
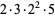 |
(5) |
 |
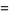 |
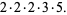 |
(6) |
The numbers of such partitions for 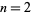 , 3, ... are 1, 1, 3, 3, 10, 10, 30, 75, 220, ... (OEIS A085288).
, 3, ... are 1, 1, 3, 3, 10, 10, 30, 75, 220, ... (OEIS A085288).
Now consider the number of such decompositions that are of length 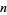 . For instance,
. For instance,
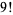 |
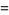 |
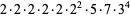 |
(7) |
 |
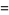 |
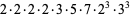 |
(8) |
 |
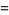 |
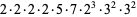 |
(9) |
 |
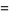 |
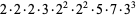 |
(10) |
 |
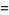 |
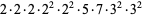 |
(11) |
 |
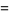 |
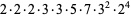 |
(12) |
 |
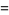 |
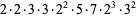 |
(13) |
 |
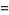 |
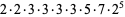 |
(14) |
 |
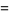 |
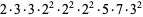 |
(15) |
 |
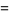 |
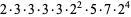 |
(16) |
 |
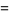 |
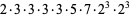 |
(17) |
 |
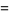 |
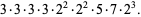 |
(18) |
The numbers of such partitions for 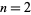 , 3, ... are 0, 0, 1, 1, 2, 2, 5, 12, 31, 31, 78, 78, 191, ... (OEIS A085289).
, 3, ... are 0, 0, 1, 1, 2, 2, 5, 12, 31, 31, 78, 78, 191, ... (OEIS A085289).
Now let
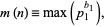 |
(19) |
i.e., 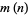 is the least prime factor raised to its appropriate power in the factorization of length
is the least prime factor raised to its appropriate power in the factorization of length 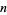 . For
. For 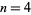 , 5, ...,
, 5, ..., 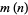 is given by 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, ... (OEIS A085290).
is given by 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, ... (OEIS A085290).
Finally, define
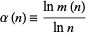 |
(20) |
where 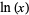 is the natural logarithm. Therefore, for the case
is the natural logarithm. Therefore, for the case 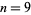 ,
, 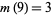 and
and
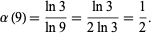 |
(21) |
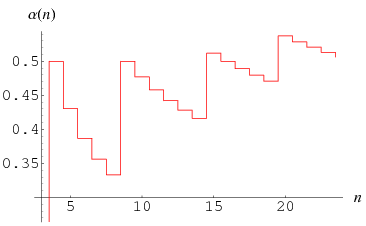
For large 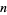 ,
, 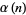 approaches a constant
approaches a constant
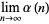 |
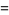 |
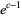 |
(22) |
 |
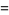 |
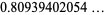 |
(23) |
(OEIS A085291), known as the Alladi-Grinstead constant, where
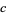 |
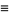 |
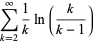 |
(24) |
 |
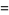 |
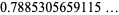 |
(25) |
(OEIS A085361). The constant 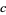 is also associated with so-called alternating Lüroth representations (Finch 2003, p. 62).
is also associated with so-called alternating Lüroth representations (Finch 2003, p. 62).
The series for 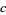 can be transformed to one with much better convergence properties by expanding the addend about infinity to get
can be transformed to one with much better convergence properties by expanding the addend about infinity to get
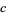 |
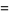 |
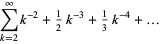 |
(26) |
 |
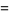 |
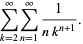 |
(27) |
Interchanging the order of summation then gives
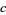 |
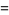 |
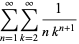 |
(28) |
 |
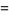 |
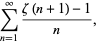 |
(29) |
where 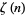 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Alladi, K. and Grinstead, C. "On the Decomposition of 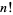 into Prime Powers." J. Number Th. 9, 452-458, 1977.
into Prime Powers." J. Number Th. 9, 452-458, 1977.
Finch, S. R. "Alladi-Grinstead Constant." §2.9 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 120-122, 2003.
Guy, R. K. "Factorial 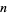 as the Product of
as the Product of 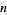 Large Factors." §B22 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 79, 1994.
Large Factors." §B22 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 79, 1994.
Sloane, N. J. A. Sequences A085288, A085289, A085290, A085291, and A085361 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|