


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-11-2020
Date: 29-10-2019
Date: 16-2-2020
|
Let 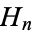 denote the
denote the 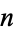 th hexagonal number and
th hexagonal number and 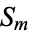 the
the 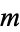 th square number, then a number which is both hexagonal and square satisfies the equation
th square number, then a number which is both hexagonal and square satisfies the equation 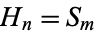 , or
, or
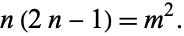 |
(1) |
Completing the square and rearranging gives
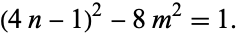 |
(2) |
Therefore, defining
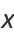 |
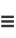 |
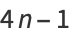 |
(3) |
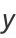 |
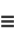 |
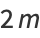 |
(4) |
gives the Pell equation
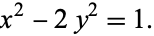 |
(5) |
The first few solutions are 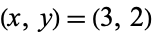 , (17, 12), (99, 70), (577, 408), .... These give the solutions
, (17, 12), (99, 70), (577, 408), .... These give the solutions 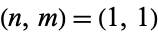 , (9/2, 6), (25, 35), (289/2, 204), ..., giving the integer solutions (1, 1), (25, 35), (841, 1189), (28561, 40391), ... (OEIS A008844 and A046176). The corresponding hexagonal square numbers are 1, 1225, 1413721, 1631432881, 1882672131025, ... (OEIS A046177).
, (9/2, 6), (25, 35), (289/2, 204), ..., giving the integer solutions (1, 1), (25, 35), (841, 1189), (28561, 40391), ... (OEIS A008844 and A046176). The corresponding hexagonal square numbers are 1, 1225, 1413721, 1631432881, 1882672131025, ... (OEIS A046177).
Closed-form solutions are
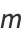 |
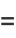 |
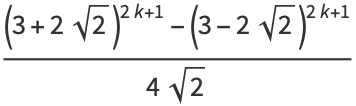 |
(6) |
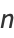 |
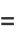 |
![1/4{1+1/2[(3-2sqrt(2))^(2k+1)+(3+2sqrt(2))^(2k+1)]},](https://mathworld.wolfram.com/images/equations/HexagonalSquareNumber/Inline19.gif) |
(7) |
giving the 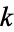 th hexagonal square number as
th hexagonal square number as
![HS_k=1/(32)[-2+(17-12sqrt(2))(3-2sqrt(2))^(4k)+(17+12sqrt(2))(3+2sqrt(2))^(4k)].](https://mathworld.wolfram.com/images/equations/HexagonalSquareNumber/NumberedEquation4.gif) |
(8) |
A recurrence relation for 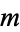 is given by
is given by
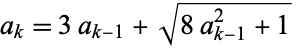 |
(9) |
with 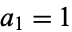 , where
, where 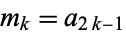 (M. Carreira, pers. comm., Sept. 11, 2004).
(M. Carreira, pers. comm., Sept. 11, 2004).
REFERENCES:
Sloane, N. J. A. Sequences A008844, A046176, and A046177 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|